题目内容
【题目】(1)问题背景
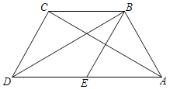
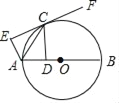
如图①,BC是⊙O的直径,点A在⊙O上,AB=AC,P为![]() 上一动点(不与B,C重合),
上一动点(不与B,C重合),
求证:![]() PA=PB+PC.
PA=PB+PC.


请你根据小明同学的思考过程完成证明过程.
(2)类比迁移
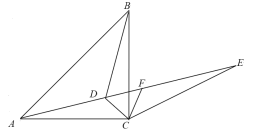
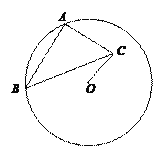
如图②,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=AC,AB⊥AC,垂足为A,求OC的最小值.

(3)拓展延伸
如图,⊙O的半径为3,点A,B在⊙O上,C为⊙O内一点,AB=![]() AC,AB⊥AC,垂足为A,则OC的最小值为 .
AC,AB⊥AC,垂足为A,则OC的最小值为 .
【答案】(1)证明见解析(2)3![]() -2(3)
-2(3)![]()
【解析】
分析: (1)将△PAC绕着点A顺时针旋转90°至△QAB(如图①),只要证明△APQ是等腰直角三角形即可解决问题,(2)如图②中,连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,在△BOQ中,利用三边关系定理即可解决问题,
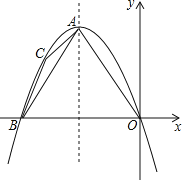
(3)如图③构造相似三角形即可解决问题,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB,
OA,连接OQ,BQ,OB,
由△QAB∽△OAC,推出BQ=![]() OC,当BQ最小时,OC最小.
OC,当BQ最小时,OC最小.
详解:(1)证明:∵BC是直径,
∴∠BAC=90°,
∵AB=AC,
∴∠ACB=∠ABC=45°,
由旋转可得∠QBA=∠PCA,∠ACB=∠APB=45°,PC=QB,
∵∠PCA+∠PBA=180°,
∴∠QBA+∠PBA=180°,
∴Q,B,P三点共线,
∴∠QAB+∠BAP=∠BAP+∠PAC=90°
∴QP2=AP2+AQ2=2AP2
∴QP=![]() AP=QB+BP=PC+PB,
AP=QB+BP=PC+PB,
∴![]() AP=PC+PB,
AP=PC+PB,
(2)解:连接OA,将△OAC绕点O顺时针旋转90°至△QAB,连接OB,OQ,
∵AB⊥AC,
∴∠BAC=90°.
由旋转可得 QB=OC.AQ=OA.∠QAB=∠OAC.
∴∠QAB+∠BAO=∠BAO+∠OAC=90°.
∴在Rt△OAQ中.OQ=3![]() ,AO=3,
,AO=3,
∴在△OQB中,BQ≥OQ-OB=3![]() -3,
-3,
即OC最小值是3![]() -3,
-3,
(3)如图中,作AQ⊥OA,使得AQ=![]() OA,连接OQ,BQ,OB,
OA,连接OQ,BQ,OB,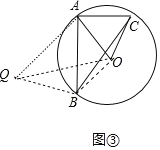
∵∠QAO=∠BAC=90°,
∠QAB=∠OAC,
∵![]() ,
,
∴△QAB∽△OAC,
∴BQ=![]() OC,
OC,
BQ最小时,OC最小,易知OA=3,AQ=4,OQ=5,BQ≥OQ-OB,
∴OQ≥2,
∴BQ的最小值为2,
∴OC的最小值为![]() ,故答案为
,故答案为![]() .
.
点睛: 本题考查圆综合题,全等三角形的判定和性质,相似三角形的判定和性质,等腰直角三角形的判定和性质,勾股定理,三角形的三边关系等知识,解题的关键是学会利用旋转法添加常用辅助线,构造全等三角形或相似三角形解决问题,属于中考压轴题.

 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案