Question

【题目】正方形的顶点，点，反比例函数

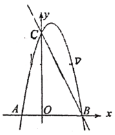
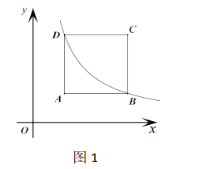
（1）如图1，双曲线经过点时求反比例函数的关系式；

　

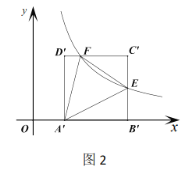
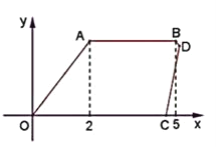
（2）如图2，正方形向下平移得到正方形边在轴上，反比例函数的图象分别交正方形的边、边于点

①求的面积；

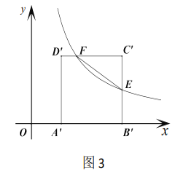
②如图3，轴上一点，是否存在是等腰三角形，若存在直接写出点坐标，若不存在请说明理由．

Answer 1

【答案】（1）；（2）①求△△A'EF的面积为；②存在，点P的坐标，，．

【解析】

（1）根据正方形的性质由点A、点C的坐标得出点D的坐标，再代入求出K的值即可；

（2）根据题意得出、的值，再代入得出E、F的值，再根据三角形的面积公式即可解答；

（3）设点P坐标为，分PF=PE,EF=EP,FP=FE三种情况，已知两点坐标根据勾股定理求两点距离，即可求出点P坐标．

（1）∵正方形ABCD的顶点A（1，1），点C（3，3）

∴点D（1，3）

则代入解得k=3·

∴

（2）∵正方形ABCD向下平移得到正方形，边在轴上，

∴(1，0)，(3，2)，，

∴代入得点E（3，1），点F（，2）

由题意可得

解得

（3）存在，利用如下：

设点P坐标为

点E（3，1），点F（，2）

，，

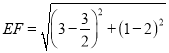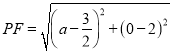
当PF=PE时，即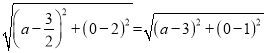

解得

此时点P的坐标为：

当EF=EP时，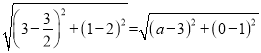

解得

此时点P的坐标为或；

当PF=FE时，

无解；

综上所述，点P坐标为：，，·