题目内容
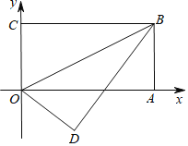
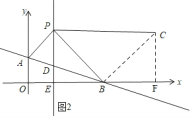
【题目】如图,在平面直角坐标系中,直线AB:y=kx+b交y轴于点A(0,1),交x轴于点B(3,0).平行于y轴的直线x=1交AB于点D,交x轴于点E,点P是直线x=1上一动点,且在点D的上方,设P(1,n).
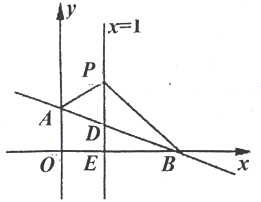
(1)求直线AB的表达式;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,直接写出点C的坐标.
【答案】(1)y=﹣![]() x+1;(2)
x+1;(2)![]() n﹣1;(3) (3,4)或(5,2)或(3,2)
n﹣1;(3) (3,4)或(5,2)或(3,2)
【解析】
(1)利用待定系数法求直线AB的解析式;
(2)根据铅直高度与水平宽度的积可得三角形的面积;
(3)先计算当S△ABP=2时,P的坐标,以PB为边在第一象限作等腰直角三角形BPC,分三种情况讨论:分别以三个顶点为直角顶点画三角形,根据图形可得C的坐标.
(1)设直线AB的解析式是y=kx+b,
把点A(0,1),点B(3,0)代入得:![]() 解得:
解得: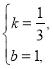 ,
,
∴直线AB的解析式是:y=﹣![]() x+1;
x+1;
(2)∵P(1,n),
∴D(1,![]() ),即PD=n﹣
),即PD=n﹣![]() ,
,
∴S△ABP=![]() PDOB=
PDOB=![]() (n﹣
(n﹣![]() )×3=
)×3=![]() n﹣1;
n﹣1;
(3)当S△ABP=2时,2=![]() n﹣1,解得n=2,
n﹣1,解得n=2,
∴点P(1,2).
∵E(1,0),
∴PE=BE=2,
∴∠EPB=∠EBP=45°
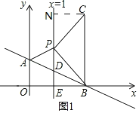
①如图1,∠CPB=90°,BP=PC,
过点C作CN⊥直线x=1于点N.
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°.
又∵∠CNP=∠PEB=90°,BP=PC,
∴△CNP≌△BEP,
∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4,
∴C(3,4).
②如图2,∠PBC=90°,BP=BC,
过点C作CF⊥x轴于点F.
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°.
又∵∠CFB=∠PEB=90°,BC=BP,
∴△CBF≌△
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5,
∴C(5,2).
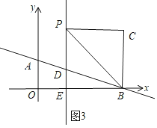
③如图3,∠PCB=90°,
∴∠CPB=∠EBP=45°,
∠CPB=∠EBP,BP=BP,∠PCB=∠PEB=90°
∴△PCB≌△BEP,
∴PC=CB=PE=EB=2,
∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,
综上所述点C的坐标是(3,4)或(5,2)或(3,2).

【题目】 在建设社会主义新农村过程中,某村委决定投资开发项目,现有6个项目可供选择,各项目所需资金及预计年利润如下表:
所需资金(亿元) | 1 | 2 | 4 | 6 | 7 | 8 |
预计利润(千万元) | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
(1)上表反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)如果预计要获得0.9千万元的利润,你可以怎样投资项目?
(3)如果该村可以拿出10亿元进行多个项目的投资,预计最大年利润是多少?说明理由.
【题目】某出租车司机从公司出发,在东西方向的人民路上连续接送![]() 批客人,行驶路程记录如下(规定向东为正,向西为负,单位:
批客人,行驶路程记录如下(规定向东为正,向西为负,单位:![]() ):
):
第 | 第 | 第 | 第 | 第 |
|
|
|
|
|
(1)接送完第![]() 批客人后,该驾驶员在公司什么方向,距离公司多少千米?
批客人后,该驾驶员在公司什么方向,距离公司多少千米?
(2)若该出租车每千米耗油![]() 升,那么在这过程中共耗油多少升?
升,那么在这过程中共耗油多少升?
(3)若该出租车的计价标准为:行驶路程不超过![]() 收费
收费![]() 元,超过
元,超过![]() 的部分按每千米
的部分按每千米![]() 元收费,在这过程中该驾驶员共收到车费多少元?
元收费,在这过程中该驾驶员共收到车费多少元?