题目内容
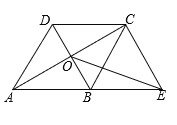
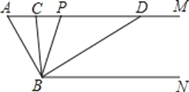
【题目】已知 
ABC(如图1)，按图2所示的尺规作图痕迹不需借助三角形全等就能推出四边形ABCD是平行四边形的依据是（ ）
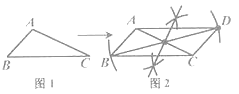
A. 两组对边分别平行的四边形是平行四边形 B. 两组对边分别相等的四边形是平行四边形
C. 一组对边平行且相等的四边形是平行四边形 D. 对角线互相平分的四边形是平行四边形
【答案】D
【解析】观察图形，可知先作线段AC的垂直平分线MN，再以O为圆心OB为半径画弧，交射线BO于点D，可证得OA=OC，OB=OD，根据对角线互相平分的四边形是平行四边形，可证得结论，即可得出答案.
根据作图可知，先作线段AC的垂直平分线MN，交AC于点O
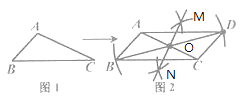
∴OA=OC，
再以O为圆心OB为半径画弧，交射线BO于点D
∴OB=OD
∴四边形ABCD是平行四边形（对角线互相平分的四边形是平行四边形）
故选：D.
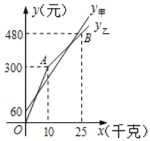
名校课堂系列答案
【题目】某学习小组在学习了函数及函数图象的知识后，想利用此知识来探究周长一定的矩形其边长分别为多少时面积最大. 请将他们的探究过程补充完整.
（1）列函数表达式：若矩形的周长为8，设矩形的一边长为x，面积为y，则有y=____________；
（2）上述函数表达式中，自变量x的取值范围是____________；
（3）列表：
x | … | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | … |
y | … | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | … |
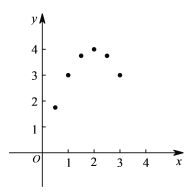
写出m=____________；
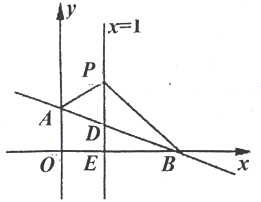
（4）画图：在平面直角坐标系中已描出了上表中部分各对应值为坐标的点，请你画出该函数的图象；
（5）结合图象可得，x=____________时，矩形的面积最大；写出该函数的其它性质（一条即可）：____________.
【题目】（1）整式
表示
、
两数和的平方
整式
表示、两数差的平方
仿照上例填空：整式
表示：______．
整式
表示：______．
（2）试计算、取不同数值时，及的值填入下表：
| 当 | 当 | 当 | 当 |
| ||||
|
（3）根据上表，我发现的规律______．
（4）用发现的规律计算：