题目内容
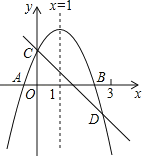
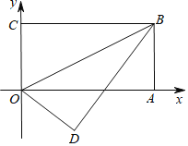
【题目】如图,四边形![]() 是矩形,点
是矩形,点![]() 的坐标为
的坐标为![]() ,点C的坐标为
,点C的坐标为![]() ,把矩形
,把矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 落在点
落在点![]() 处,则点
处,则点![]() 的纵坐标为( )
的纵坐标为( )
A. -2B. -2.4C. -2![]() D. -2
D. -2![]()
【答案】B
【解析】
由折叠的性质得到一对角相等,再由矩形对边平行得到一对内错角相等,等量代换及等角对等边得到BE=OE,利用AAS得到三角形OED与三角形BEA全等,由全等三角形对应边相等得到DE=AE,过D作DF垂直于OE,利用勾股定理及面积法求出DF与OF的长,即可确定出D坐标.
解:由折叠得:∠CBO=∠DBO,
∵矩形ABCO,
∴BC∥OA,
∴∠CBO=∠BOA,
∴∠DBO=∠BOA,
∴BE=OE,
在△ODE和△BAE中,
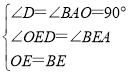 ,
,
∴△ODE≌△BAE(AAS),
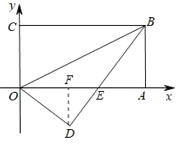
∴AE=DE,
设DE=AE=x,则有OE=BE=8x,
在Rt△ODE中,根据勾股定理得:42+x2=(8x)2,
解得:x=3,即OE=5,DE=3,
过D作DF⊥OA,
∵S△OED=![]() ODDE=
ODDE=![]() OEDF,
OEDF,
∴DF=![]()
∴点![]() 的纵坐标为-
的纵坐标为-![]() =-2.4,
=-2.4,
故选B.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目