��Ŀ����
����Ŀ�� �ڽ������������ũ������У�ij��ί����Ͷ�ʿ�����Ŀ������6����Ŀ�ɹ�ѡ����Ŀ�����ʽ�Ԥ�����������±���
�����ʽ���Ԫ�� | 1 | 2 | 4 | 6 | 7 | 8 |
Ԥ������ǧ��Ԫ�� | 0.2 | 0.35 | 0.55 | 0.7 | 0.9 | 1 |
��1���ϱ���ӳ������������֮��Ĺ�ϵ���ĸ����Ա������ĸ����������
��2�����Ԥ��Ҫ���0.9ǧ��Ԫ���������������Ͷ����Ŀ��
��3������ô�����ó�10��Ԫ���ж����Ŀ��Ͷ�ʣ�Ԥ������������Ƕ��٣�˵�����ɣ�
���𰸡���1�������ʽ������֮��Ĺ�ϵ�������ʽ�Ϊ�Ա�����������Ϊ���������2������Ͷ��һ��7��Ԫ����Ŀ��Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ����3�����������1.45��Ԫ���������������
��������
��1���ֱ���ݱ�����������Ķ���ֱ�ó����ɣ�
��2������ͼ�������ó�Ͷ�ʷ�����
��3���ֱ������ͬ��������������ó��𰸣�
�⣺��1�������ʽ������֮��Ĺ�ϵ��
�����ʽ�Ϊ�Ա�����������Ϊ�������
��2������Ͷ��һ��7��Ԫ����Ŀ��
Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��
������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ��
�𣺿���Ͷ��һ��7��Ԫ����Ŀ��Ҳ����Ͷ��һ��2��Ԫ����Ͷ��һ��4��Ԫ����Ŀ��������Ͷ��һ��1��Ԫ����Ͷ��һ��6��Ԫ����Ŀ��
��3�������ַ�������1��Ԫ��2��Ԫ��7��Ԫ��������![]() ��Ԫ��
��Ԫ��
��2��Ԫ��8��Ԫ��������![]() ��Ԫ��
��Ԫ��
��4��Ԫ��6��Ԫ��������![]() ��Ԫ��
��Ԫ��
�����������![]() ��Ԫ��
��Ԫ��
�����������![]() ��Ԫ��
��Ԫ��

 ������ѧ���̲���ȫ���ϵ�д�
������ѧ���̲���ȫ���ϵ�д� ������ʱ����ҵ����ϵ�д�
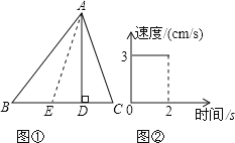
������ʱ����ҵ����ϵ�д�����Ŀ��ijѧϰС����ѧϰ�˺���������ͼ���֪ʶ�������ô�֪ʶ��̽���ܳ�һ���ľ�����߳��ֱ�Ϊ����ʱ������. �뽫���ǵ�̽�����̲�������.
��1���к�������ʽ�������ε��ܳ�Ϊ8������ε�һ�߳�Ϊx�����Ϊy������y=____________��
��2��������������ʽ�У��Ա���x��ȡֵ��Χ��____________��
��3�����
x | �� | 0.5 | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 | �� |
y | �� | 1.75 | 3 | 3.75 | 4 | 3.75 | 3 | m | �� |
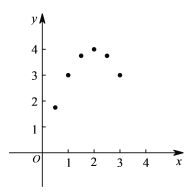
�m=____________��
��4����ͼ����ƽ��ֱ������ϵ����������ϱ��в��ָ���ӦֵΪ����ĵ㣬���㻭���ú�����ͼ��
��5�����ͼ��ɵã�x=____________ʱ�����ε�������д���ú������������ʣ�һ�����ɣ���____________.