题目内容
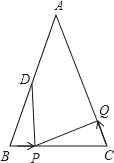
【题目】如图,已知△ABC中,AB=6cm,∠B=∠C,BC=4cm,点D为AB的中点.若点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
【答案】(1)全等(2)vQ=1.5cm/s
【解析】试题分析:(1)根据时间和速度分别求得两个三角形中BP、CQ和BD、PC边的长,根据SAS判定两个三角形全等.
(2)根据全等三角形应满足的条件探求边之间的关系,再根据路程=速度×时间公式,先求得点P运动的时间,再求得点Q的运动速度;
试题解析:解:(1)全等,理由如下:
∵t=1秒,∴BP=CQ=1×1=1厘米,∵AB=6cm,点D为AB的中点,∴BD=3cm.
又∵PC=BC﹣BP,BC=4cm,∴PC=4﹣1=3cm,∴PC=BD.
∵∠B=∠C,∴△BPD≌△CPQ;
(2)∵vP≠vQ,∴BP≠CQ,又∵△BPD≌△CPQ,∠B=∠C,则BP=CP=2,BD=CQ=3,∴点P,点Q运动的时间为:t=2秒,∴vQ=1.5cm/s;

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目