Question

【题目】定义：如果一个三角形一条边上的高与这条边的比值是，那么称这个三角形为“准黄金”三角形，这条边就叫做这个三角形的“金底”．

（1）如图，在△ABC中，AC=8，BC=5，，试判断△ABC是否是“准黄金”三角形，请说明理由．

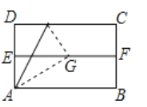
（2）如图，△ABC是“准黄金”三角形，BC是“金底”，把△ABC沿BC翻折得到△DBC，AD交BC的延长线于点E，若点C恰好是△ABD的重心，求的值．

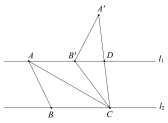
（3）如图，，且直线与之间的距离为4，“准黄金”△ABC的“金底”BC在直线上，点A在直线上，=，若∠ABC是钝角，将△ABC绕点C按顺时针方向旋转得到△，线段交于点D．当点落在直线上时，则的值为____．

Answer 1

【答案】（1）△ABC是“准黄金”三角形；理由见解析；（2）；（3）

【解析】

(1)过点A作AD⊥CB交CB的延长线于D．解直角三角形求出AD即可得出结论．

(2) 根据A，D关于BC对称，得到BE⊥AD，AE＝ED，根据△ABC是“准黄金”三角形，得到BC是“金底”，再利用C是△ABD的重心求解即可得到答案；

(3) 过点A作AE⊥BC于E，过点D作DF⊥AC于F，过点B′作B′G⊥BC于G．证明△CGB′∽△CFD，推出DF：CF：CD=GB′：CG：CB′=4：3：5，设DF=4k，CF=3k，CD=5k，再求出AD（用k表示）即可解决问题．

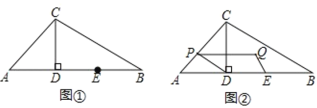
解：（1）结论：△ABC是“准黄金”三角形，BC是“金底”．

理由：过点A作AD⊥CB交CB的延长线于D．

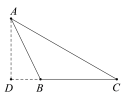
∵AC＝8，∠C＝30°，

∴AD＝4，

∴＝

∴△ABC是“准黄金”三角形，BC是“金底”；

（2）如图，

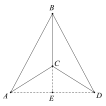
∵A，D关于BC对称，

∴BE⊥AD，AE＝ED，

∵△ABC是“准黄金”三角形，BC是“金底”，

∴＝，不妨设AE＝4k，BC＝5k，

∵C是△ABD的重心，

∴BC：CE＝2：1，

∴CE＝ ，BE＝ ，

∴AB＝，

∴；

（3）如图4中，过点A作AE⊥BC于E，过点D作DF⊥AC于F，过点B′作B′G⊥BC于G．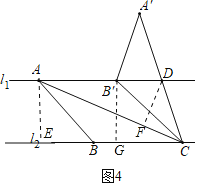

在Rt△CB′G中，∵∠CGB′=90°，GB′=4，=CB=5，

∴ ，

又∵=，

∴ ，

∴ ，

∴EC=7，

∵∠GCB′=∠FCD=α，∠CGB′=∠CFD=90°，
∴△CGB′∽△CFD，
∴DF：CF：CD=GB′：CG：CB′=4：3：5，
设DF=4k，CF=3k，CD=5k，
∵△AEC∽△DFA，

，

解得： ，

∴AF=7k，

∴

．