Question

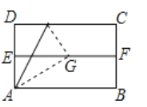
【题目】如图，矩形ABCD中，AB=4，AD=3，∠DAB的角平分线交边CD于点E．点P在射线AE上以每秒个单位长度的速度沿射线AE方向从点A开始运动；过点P作PQ⊥AB于点Q，以PQ为边向右作平行四边形，点N在射线AE上，且AP=PN．设P点运动时间为t秒．

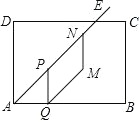
（1）PQ= （用含t的代数式表示）．

（2）当点M落在BC边上时，求t的值．

（3）设平行四边形PQMN与矩形ABCD重合部分面积为S，当点P在线段AE上运动时，求S与t 的函数关系式．

（4）直接写出在点P、Q运动的过程中，整个图形中形成的三角形存在全等三角形时t的值（不添加任何辅助线）．

Answer 1

【答案】（1）t；（2）2；（3）当0≤t≤时，；当≤2时，；当≤3时，；（4）2或3或

【解析】

（1）判断出ΔAPQ是等腰三角形即可得出结结论；

（2）由AP=PN判断出Q为AB的中点，进而求得AQ=2，即可得出结论；

（3）分三种情况讨论：①当0﹤t≤时，重合部分是平行四边形PQMN；②当≤2时，重合部分是五边形PQMGE，③当≤3时，重合部分是五边形PQGCE，分别求解即可；

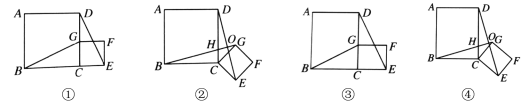
（4）也是分三种情况讨论：①当点Q是AB的中点时，ΔAPQ≌ΔQMB；②当点P与点E重合时，ΔAPQ≌ΔEAD；③当ΔPEK≌ΔQGB时，分别求解即可.

（1）∵四边形ABCD是矩形，

∴∠BAD=90，

∵AE平分∠BAD，

∴∠BAE=45，

∵PQ⊥AB，

∴ΔAPQ是等腰直角三角形，

由运动知，AP=t，

∴PQ= t；

（2）如图2，当点M落在BC上时，

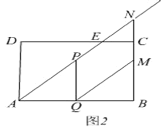
∵四边形PQMN是平行四边形，

∴PQ∥MN，即PQ∥BN,

∵AP=PN，

∴AQ=QB=2．

∵∠NAB =45°，

∴PQ=AQ=2．

∴t=2

（3）①当0≤t≤时，如图4，重合部分是平行四边形PQMN，；

②当≤2时，如图5，重合部分是五边形PQMGE，

；

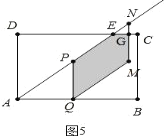
③当≤3时，如图6，重合部分是五边形PQGCE，

=，

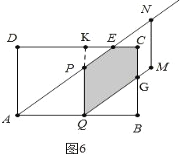
综上，当0≤t≤时，；当≤2时，；当≤3时，；．

（4）①如图7，当点Q是AB的中点时，ΔAPQ≌ΔQMB，此时；

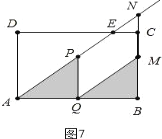
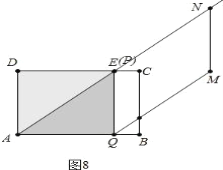
②如图8，当点P与点E重合时，ΔAPQ≌ΔEAD，，

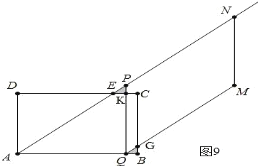
③如图9，当ΔPEK≌ΔQGB时，由EK=BQ得：t-3=4-t，解得．

综上，t的值为2或3或．