题目内容
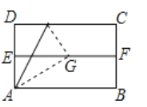
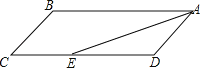
【题目】如图,四边形ABCD为平行四边形,AD=2,AB=6,∠DAB=60°,E为边CD上一点.
(1)尺规作图:延长AE,过点C作射线AE的垂线,垂足为F(不写作法,保留作图痕迹);
(2)当点E在线段CD上(不与C,D重合)运动时,求EFAE的最大值.
【答案】(1)见解析;(2)![]()
【解析】
(1)利用尺规作CF⊥AE交AE的延长线于F即可.
(2)作AH⊥CD交CD的延长线于H.设EC=x.解直角三角形求出DH,证明△CFE∽△AHE,推出![]() =
=![]() ,推出EFAE=CEEH=x(7﹣x)=﹣x2+7x=﹣(x﹣
,推出EFAE=CEEH=x(7﹣x)=﹣x2+7x=﹣(x﹣![]() )2+
)2+![]() ,再利用二次函数的性质求解即可.
,再利用二次函数的性质求解即可.
解:(1)如图,射线CF即为所求.
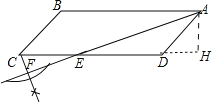
(2)作AH⊥CD交CD的延长线于H.设EC=x.
∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=6,
∴∠BAD=∠ADH=60°,
∵∠H=90°,
∴∠DAH=30°,
∴DH=![]() AD=1,
AD=1,
∴CH=CD+DH=6+1=7,
∵∠CFE=∠H=90°,∠CEF=∠AEH,
∴△CFE∽△AHE,
∴![]() =
=![]() ,
,
∴EFAE=CEEH=x(7﹣x)=﹣x2+7x=﹣(x﹣![]() )2+
)2+![]() ,
,
∵﹣1<0,
∴EFAE的最大值为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目