Question

【题目】探究与应用．试完成下列问题：
（1）如图①，已知等腰Rt△ABC中，∠C=90°，点O为AB的中点，作∠POQ=90°，分别交AC、BC于点P、Q，连结PQ、CO，求证：AP2+BQ2=PQ2；
（2）如图②，将等腰Rt△ABC改为任意直角三角形，点O仍为AB的中点，∠POQ=90°，试探索上述结论AP2+BQ2=PQ2是否仍成立；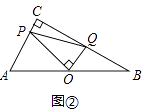
（3）通过上述探究（可直接运用上述结论），试解决下面的问题：如图③，已知Rt△ABC中，∠C=90°，AC=6，BC=8，点O为AB的中点，过C、O两点的圆分别交AC、BC于P、Q，连结PQ，求△PCQ面积的最大值．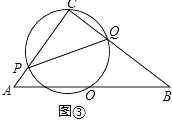

Answer 1

【答案】
（1）证明：∵△ABC是等腰直角三角形，O为斜边AB中点，

∴AO=OC=OB，∠A=∠B=∠OCQ=45°，∠AOC=90°，

∵∠POQ=90°，

∴∠AOP+∠POC=∠POC+∠COQ，

∴∠AOP=∠COQ，

在△AOP和△COQ中

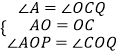
∴△AOP≌△COQ，

∴AP=CQ，

同理BQ=CP，

在Rt△CPQ中，CP2+CQ2=PQ2，

∴AP2+BQ2=PQ2

（2）解：还成立，

理由是：延长QO到D，使OD=OQ，连接AD，PD，

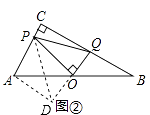
∵O是AB中点，

∴AO=OB，

在△AOD和△BOQ中

∴△AOD≌△BOQ（SAS），

∴AD=BQ，∠BAD=∠B，OD=OQ，

∵PO⊥OQ，

∴PD=PQ，

∵∠C=90°，

∴∠PAD=90°，

在Rt△PAD中，由勾股定理得：AP2+AD2=PD2，

∴AP2+BQ2=PQ2

（3）解：∵∠C=90°，

∴PQ是直径，

连接PO、OQ，则∠POQ=90°，

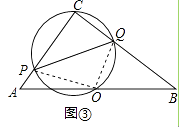
∴AP2+BQ2=PQ2，

设PC=a，CQ=b，

∴（6﹣a）2+（8﹣b）2=a2+b2，

∴3a+4b=25，

∴b=﹣ a+ ，

∵S△PCQ= ab，

∴S△PCQ=﹣ a2+ a=﹣ （a﹣ ）2+ ．

当a= 时，△PCQ的面积的最大值是

【解析】（1）证△APO≌△COQ，求出AP=CQ，同理求出BQ=CP，根据勾股定理求出即可；（2）延长QO到D，使OD=OQ，连接AD，PD，求出PD=PQ，证△AOD≌△BOQ，推出AD=BQ，∠BAD=∠B，OD=OQ，在Rt△PAD中，由勾股定理得：AP2+AD2=PD2 ， 即可得出答案；（3）连接PO、OQ，则∠POQ=90°，根据勾股定理得出AP2+BQ2=PQ2 ， 设PC=a，CQ=b，推出（6﹣a）2+（8﹣b）2=a2+b2 ， 求出b=﹣ a+ ，代入S△PCQ= ab求出即可．