Question

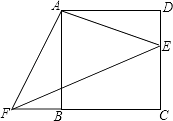
【题目】如图，四边形ABCD内接于⊙O，BD是⊙O的直径，AE⊥CD，垂足为E，DA平分∠BDE．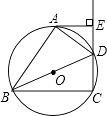
（1）求证：AE是⊙O的切线；
（2）若∠DBC=30°，DE=1cm，求BD的长．

Answer 1

【答案】
（1）证明：连接OA，

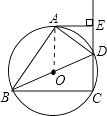
∵DA平分∠BDE，

∴∠BDA=∠EDA．

∵OA=OD，

∴∠ODA=∠OAD，

∴∠OAD=∠EDA，

∴OA∥CE．

∵AE⊥CE，

∴AE⊥OA．

∴AE是⊙O的切线

（2）解：∵BD是直径，

∴∠BCD=∠BAD=90°．

∵∠DBC=30°，∠BDC=60°，

∴∠BDE=120°．

∵DA平分∠BDE，

∴∠BDA=∠EDA=60°．

∴∠ABD=∠EAD=30°．

∵在Rt△AED中，∠AED=90°，∠EAD=30°，

∴AD=2DE．

∵在Rt△ABD中，∠BAD=90°，∠ABD=30°，

∴BD=2AD=4DE．

∵DE的长是1cm，

∴BD的长是4cm．

【解析】（1）连接OA，根据角之间的互余关系可得∠OAE=∠DEA=90°，故AE⊥OA，即AE是⊙O的切线；（2）根据圆周角定理，可得在Rt△AED中，∠AED=90°，∠EAD=30°，有AD=2DE；在Rt△ABD中，∠BAD=90°，∠ABD=30°，有BD=2AD=4DE，即可得出答案．