题目内容
【题目】点![]() 的“
的“![]() 值”定义如下:若点
值”定义如下:若点![]() 为圆上任意一点,线段
为圆上任意一点,线段![]() 长度的最大值与最小值之差即为点
长度的最大值与最小值之差即为点![]() 的“
的“![]() 值”,记为
值”,记为![]() .特别的,当点
.特别的,当点![]() ,
, ![]() 重合时,线段
重合时,线段![]() 的长度为0.
的长度为0.
当⊙![]() 的半径为2时:
的半径为2时:
(1)若点![]() ,
, ![]() ,则
,则![]() _________,
_________, ![]() _________;
_________;
(2)若在直线![]() 上存在点
上存在点![]() ,使得
,使得![]() ,求出点
,求出点![]() 的横坐标;
的横坐标;
(3)直线![]() 与
与![]() 轴,
轴, ![]() 轴分别交于点
轴分别交于点![]() ,
, ![]() .若线段
.若线段![]() 上存在点
上存在点![]() ,使得
,使得![]() ,请你直接写出
,请你直接写出![]() 的取值范围.
的取值范围.

【答案】(1)1;4(2)-1或-![]() (3)
(3)![]()
【解析】试题分析:(1)根据定义求解即可;
(2)根据定义知:满足dP=2的点位于一点O为圆心,半径为1的圆周上,设P(a,2a+2),由PO=1,建立方程求解即可;
(3)根据题意可知,满足2≤dP<3的点位于以点O为圆心,外径为![]() ,内径为1的圆环内.
,内径为1的圆环内.
分别求出当线段与外环相切或内切时, b的值即可.
试题解析:解:(1)dC=1,dD=4;
(2)根据题意,满足dP=2的点位于一点O为圆心,半径为1的圆周上.
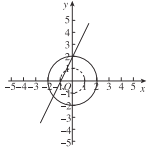
∵点P在直线y=2x+2上,∴设P(a,2a+2).
∵PO=1,∴a2+(2a+2)2=1,解得a=-1或a=![]() ,∴xP=-1或
,∴xP=-1或![]() .
.
(3)![]() .解析如下:
.解析如下:
根据题意,满足2≤dP<3的点位于以点O为圆心,外径为![]() ,内径为1的圆环内.
,内径为1的圆环内.
当线段与外环相切时,解得b=![]() ;
;
当线段与内环相切时,解得b=![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目