题目内容
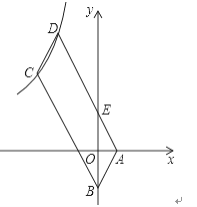
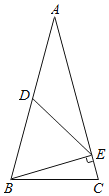
【题目】如图,已知AB∥CD,现将一直角三角形PMN放入图中,其中∠P=90°,PM交AB于点E,PN交CD于点F
(1)当△PMN所放位置如图①所示时,则∠PFD与∠AEM的数量关系为 ;
(2)当△PMN所放位置如图②所示时,求证:∠PFD﹣∠AEM=90°;
(3)在(2)的条件下,若MN与CD交于点O,且∠DON=30°,∠PEB=15°,求∠N的度数.

【答案】(1)∠PFD+∠AEM=90°(2)证明见解析(3)45°
【解析】分析:(1)由AB∥CD可得∠PFD与∠AEM的等于∠P;(2)∠1+∠PFD=180°,由对顶角相等,分别将∠1,∠AEM转化为∠PHE与∠2;(3)由∠PEB=15°得∠PHE和∠1,又AB∥CD,则∠1=∠PFC,而∠PFC=∠N+∠DON.
详解:(1)过P作平行线,由AB∥CD易得∠PFD与∠AEM的等于∠P,所以∠PFD与∠AEM的数量关系为 ∠PFD+∠AEM=90° ;
(2)证明:如图②所示:
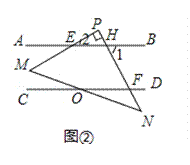
∵AB∥CD,∴∠PFD+∠1=180°,
∵∠P=90°,∴∠PHE+∠2=90°,
∵∠2=∠AEM,∴∠1=∠PHE=90°﹣∠AEM,
∴∠PFD+90°﹣∠AEM=180°,
∴∠PFD﹣∠AEM=90°;
(3)如图②所示:
∵∠P=90°,∴∠PHE=90°﹣∠PEB=90°﹣15°=75°,
∵AB∥CD,∴∠PFC=∠PHE=75°,
∵∠PFC=∠N+∠DON,
∴∠N=75°﹣30°=45°.

【题目】某校八年级学生在学习《数据的分析》后,进行了检测,现将该校八(1)班学生的成绩统计如下表,并绘制成条形统计图(不完整). 
分数(分) | 人数(人) |
68 | 4 |
78 | 7 |
80 | 3 |
88 | 5 |
90 | 10 |
96 | 6 |
100 | 5 |
(1)补全条形统计图;
(2)该班学生成绩的平均数为86.85分,写出该班学生成绩的中位数和众数;
(3)该校八年级共有学生500名,估计有多少学生的成绩在96分以上(含96分)?
(4)小明的成绩为88分,他的成绩如何,为什么?