题目内容
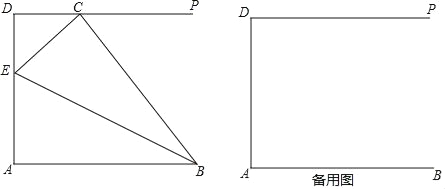
【题目】如图,线段AB=5,AD=4,∠A=90°,DP∥AB,点C为射线DP上一点,BE平分∠ABC交线段AD于点E(不与端点A、D重合).
(1)当∠ABC为锐角,且tan∠ABC=2时,求四边形ABCD的面积;
(2)当△ABE与△BCE相似时,求线段CD的长;
(3)设CD=x,DE=y,求y关于x的函数关系式,并写出定义域.
【答案】(1)16(2)当△ABE∽△EBC时,线段CD的长为2或![]() (3)
(3)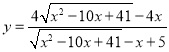 (0<x<4.1)
(0<x<4.1)
【解析】试题分析:(1) 过C作CH⊥AB与H,由∠A=90°,DP∥AB,可得得四边形ADCH为矩形,在△BCH中,CH=AD=4,∠BHC=90°,tan∠CBH=2,得HB=CH÷2=2, 所以CD=AH=5-2=3,
则四边形ABCD的面积=![]() ,
,
(2) 由BE平分∠ABC,得∠ABE=∠EBC,当△ABE∽△EBC时,
∠BCE=∠BAE=90°,由BE=BE,得△BEC≌△BEA,得BC=BA=5,在△BCH中,BH=![]() ,所以CD=AH=5-3=2.
,所以CD=AH=5-3=2.
∠BEC=∠BAE=90°,延长CE交BA延长线于T,由∠ABE=∠EBC,
∠BEC=∠BET=90°,BE=BE,得△BEC≌△BET,得BC=BT,且CE=TE,又CD∥AT,得AT=CD.令CD=x,则在△BCH中,BC=BT=5+x,BH=5-x,∠BHC=90°,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
(3) 延长BE交CD延长线于M,因为AB∥CD,所以∠M=∠ABE=∠CBM,所以CM=CB,
在△BCH中,由勾股定理可得: ![]() ,
,
则DM=CM-CD= ![]() ,又因为DM∥AB,可得
,又因为DM∥AB,可得![]() ,即
,即![]() ,
,
即可得到: 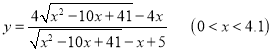 .
.
试题解析:(1)过C作CH⊥AB与H,
由∠A=90°,DP∥AB,得四边形ADCH为矩形,
在△BCH中,CH=AD=4,∠BHC=90°,tan∠CBH=2,得HB=CH÷2=2,
所以CD=AH=5-2=3,
则四边形ABCD的面积=![]() ,
,
(2)由BE平分∠ABC,得∠ABE=∠EBC,
当△ABE∽△EBC时,
∠BCE=∠BAE=90°,由BE=BE,得△BEC≌△BEA,得BC=BA=5,
于是在△BCH中,BH=![]() ,
,
所以CD=AH=5-3=2.
∠BEC=∠BAE=90°,延长CE交BA延长线于T,
由∠ABE=∠EBC,∠BEC=∠BET=90°,BE=BE,得△BEC≌△BET,得BC=BT,
且CE=TE,又CD∥AT,得AT=CD.
令CD=x,则在△BCH中,BC=BT=5+x,BH=5-x,∠BHC=90°,
所以![]() ,即
,即![]() ,解得
,解得![]() ,
,
综上,当△ABE∽△EBC时,线段CD的长为2或![]() .
.
(3)延长BE交CD延长线于M,
由AB∥CD,得∠M=∠ABE=∠CBM,所以CM=CB,
在△BCH中, ![]() ,
,
则DM=CM-CD= ![]() ,
,
又DM∥AB,得![]() ,即
,即![]() ,
,
解得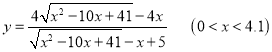 .
.