题目内容
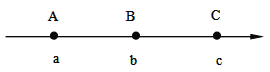
【题目】有理数a、b、c在数轴上的位置如图:
![]()
(1)用不等号填空:-b 0,|c| 0,|a| |b|,b-c 0,a+b 0,c-a 0.
(2)化简:![]()
【答案】(1)<,>,>,<,<,>(2)-2b
【解析】
(1)把-b,|c|,|a|,|b|在数轴上表示出来,根据数轴上右边的大于左边的数判断大小.两个数相减判断正负时,大数减小数为正,小数减大数为负.两数相加判断正负时,同正则为正,同负则为负,一正一负时,若负数的绝对值大则和为负,若正数绝对值大则和为正.
(2)首先判断绝对值内的正负情况,再根据正数的绝对值是它本身,负数的绝对值是它的相反数的规律去绝对值.最后合并同类项.
(1) -b,|c|,|a|,|b|在数轴上表示出来:
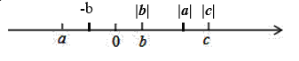
根据数轴上右边的大于左边的数可知:-b<0,|c|>0,|a|>|b|
b小于c,则b-c<0;c大于a,则c-a>0.
a是负数,a的绝对值大于b,则a+b<0.
(2)b-c<0,则 ![]() ,c-a>0,则
,c-a>0,则![]() ,a+b<0,则
,a+b<0,则
![]()
则原式=c-b+(-a-b)-(c-a)=-2b
故答案为:(1)<,>,>,<,<,>(2)-2b

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目