题目内容
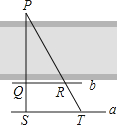
【题目】如图，点M是直线y=2x+3上的动点，过点M作MN垂直于x轴于点N，y轴上是否存在点P，使得△MNP为等腰直角三角形，则符合条件的点P有（提示：直角三角形斜边上的中线等于斜边的一半）（ ）
A. 2个 B. 3个 C. 4个 D. 5个
【答案】C
【解析】
根据等腰直角三角形的定义,由题意,应分两类情况讨论：当MN为直角边时和当MN为斜边时点Ｐ的位置的求法．
当M运动到(－1，1)时，ON=1，MN=1，
∵MN⊥x轴，所以由ON=MN可知，(0，0)和(0，1)就是符合条件的P点；
又当M运动到第三象限时，要MN=MP，且PM⊥MN，设点M(x，2x+3)，则有－x=－(2x+3)，解得x=－3，所以点P坐标为(0，－3)．
如若MN为斜边时，则∠ONP=45°，所以ON=OP，设点M(x，2x+3)，则有－x=－
(2x+3)，化简得－2x=－2x－3，这方程无解，所以这时不存在符合条件的P点；
又当点M′在第二象限，M′N′为斜边时，这时N′P=M′P，∠M′N′P=45°，设点M′(x，2x+3)，则OP=ON′，而OP=M′N′，∴有－x=(2x+3)，解得x=－
，这时点P的坐标为(0，－)．
因此，符合条件的点P坐标是(0，0)，(0，－)，(0，－3)，(0，1)．
故答案选C,
名师指导期末冲刺卷系列答案
开心蛙口算题卡系列答案
【题目】下面是某同学对多项式（x2－4x+2）（x2－4x+6）+4进行因式分解的过程．
解：设x2－4x=y
原式=（y+2）（y+6）+4 （第一步）
=y2+8y+16 （第二步）
=（y+4）2（第三步）
=（x2－4x+4）2（第四步）
回答下列问题：
（1）该同学第二步到第三步运用了因式分解的_______．
A．提取公因式 |
B．平方差公式 |
C．两数和的完全平方公式 |
D．两数差的完全平方公式 |
（2）该同学因式分解的结果是否彻底？________．（填“彻底”或“不彻底”）若不彻底，请直接写出因式分解的最后结果_________ ．
（3）请你模仿以上方法尝试对多项式（x2－2x）（x2－2x+2）+1进行因式分解．
