题目内容
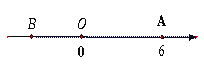
【题目】我们知道,![]() 表示数
表示数![]() 在数轴上的对应点与原点的距离.如:
在数轴上的对应点与原点的距离.如:![]() 表示
表示![]() 在数轴上的对应点到原点的距离.而
在数轴上的对应点到原点的距离.而![]() ,即
,即![]() 表示
表示![]() 和
和![]() 在数轴上对应的两点之间的距离.类似的,有:
在数轴上对应的两点之间的距离.类似的,有:![]() 表示
表示![]() 和
和![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 和
和![]() 在数轴上对应的两点之间的距离.一般地,点
在数轴上对应的两点之间的距离.一般地,点![]() 在数轴上分别表示数
在数轴上分别表示数![]() 和
和![]() ,那么点
,那么点![]() 和
和![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
利用以上知识:
(1)求代数式![]()
![]() 的最小值
的最小值![]() .
.
(2)求代数式![]()
![]() 的最小值.
的最小值.
【答案】(1)2500;(2)![]() .
.
【解析】
(1)根据绝对值的几何意义,可知:x=50.5时,![]()
![]() 取最小值,即可求解;
取最小值,即可求解;
(2)由![]()
![]()
![]() ,进而根据绝对值的几何意义,即可求解.
,进而根据绝对值的几何意义,即可求解.
(1)∵![]()
![]() =数轴上x所对应的点到点1,2,3,…,100的距离之和,
=数轴上x所对应的点到点1,2,3,…,100的距离之和,
∴当x所对应的点在点1和点100的最中间时,![]()
![]() 取最小值,即x=50.5时,
取最小值,即x=50.5时,![]()
![]() 取最小值,
取最小值,
此时,![]()
![]() 的最小值
的最小值
=![]()
![]() =2500,
=2500,
故答案是:2500;
(2)![]()
![]()
![]()
![]()
![]()
∵![]() =数轴上x所对应的点到点1,1,…1,2,2,2,2,2,2,9,9,9,9,16,16,16的距离之和,
=数轴上x所对应的点到点1,1,…1,2,2,2,2,2,2,9,9,9,9,16,16,16的距离之和,
∴x=2时,![]() 取最小值,
取最小值,
此时,![]() 最小值
最小值
=![]() =82,
=82,
∴![]()
![]() 的最小值=
的最小值=![]()
![]() .
.
故答案是:![]() .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目