Question

【题目】如图，已知矩形OABC中，OA=2，AB=4，双曲线 （k＞0）与矩形两边AB、BC分别交于E、F．

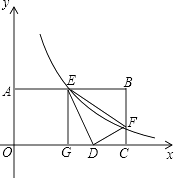
（1）若E是AB的中点，求F点的坐标；
（2）若将△BEF沿直线EF对折，B点落在x轴上的D点，作EG⊥OC，垂足为G，证明△EGD∽△DCF，并求k的值．

Answer 1

【答案】
（1）

解：∵点E是AB的中点，OA=2，AB=4，

∴点E的坐标为（2，2），

将点E的坐标代入y= ，可得k=4，

即反比例函数解析式为：y= ，

∵点F的横坐标为4，

∴点F的纵坐标= =1，

故点F的坐标为（4，1）

（2）

解：由折叠的性质可得：BE=DE，BF=DF，∠B=∠EDF=90°，

∵∠CDF+∠EDG=90°，∠GED+∠EDG=90°，

∴∠CDF=∠GED，

又∵∠EGD=∠DCF=90°，

∴△EGD∽△DCF，

结合图形可设点E坐标为（ ，2），点F坐标为（4， ），

则CF= ，BF=DF=2﹣ ，ED=BE=AB﹣AE=4﹣ ，

在Rt△CDF中，CD= = = ，

∵ ，即 = ，

∴ =1，

解得：k=3

【解析】（1）根据点E是AB中点，可求出点E的坐标，将点E的坐标代入反比例函数解析式可求出k的值，再由点F的横坐标为4，可求出点F的纵坐标，继而得出答案；（2）证明∠GED=∠CDF，然后利用两角法可判断△EGD∽△DCF，设点E坐标为（ ，2），点F坐标为（4， ），即可得CF= ，BF=DF=2﹣ ，在Rt△CDF中表示出CD，利用对应边成比例可求出k的值．
【考点精析】本题主要考查了反比例函数的图象和反比例函数的性质的相关知识点，需要掌握反比例函数的图像属于双曲线．反比例函数的图象既是轴对称图形又是中心对称图形．有两条对称轴：直线y=x和 y=-x．对称中心是：原点；性质:当k＞0时双曲线的两支分别位于第一、第三象限，在每个象限内y值随x值的增大而减小； 当k＜0时双曲线的两支分别位于第二、第四象限，在每个象限内y值随x值的增大而增大才能正确解答此题．