题目内容
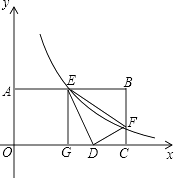
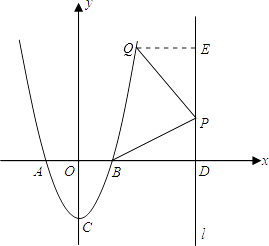
【题目】如图，二次函数y=ax2+bx+c的图象的顶点C的坐标为（0，﹣2），交x轴于A、B两点，其中A（﹣1，0），直线l：x=m（m＞1）与x轴交于D．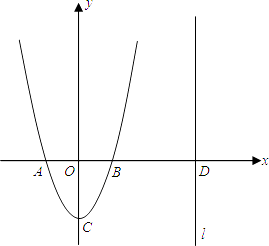
（1）求二次函数的解析式和B的坐标；
（2）在直线l上找点P（P在第一象限），使得以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似，求点P的坐标（用含m的代数式表示）；
（3）在（2）成立的条件下，在抛物线上是否存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形？如果存在，请求出点Q的坐标；如果不存在，请说明理由．
【答案】
（1）
解：∵抛物线y=ax2+bx+c的顶点坐标为C（0，﹣2），
∴b=0，c=﹣2；
∵y=ax2+bx+c过点A（﹣1，0），
∴0=a+0﹣2，a=2，
∴抛物线的解析式为y=2x2﹣2．
当y=0时，2x2﹣2=0，
解得x=±1，
∴点B的坐标为（1，0）
（2）
解：设P（m，n）．
∵∠PDB=∠BOC=90°，
∴当以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似时，分两种情况：
① 若△OCB∽△DBP，则 
，
即 
= 
，
解得n= 
．
由对称性可知，在x轴上方和下方均有一点满足条件，
∴此时点P坐标为（m， ）或（m， 
），
∵点P在第一象限，
∴点P的坐标为（m， ）
②若△OCB∽△DPB，则 ，
即 
= 
，
解得n=2m﹣2．
由对称性可知，在x轴上方和下方均有一点满足条件，
∴此时点P坐标为（m，2m﹣2）或（m，2﹣2m），
∵P在第一象限，m＞1，
∴点P的坐标为（m，2m﹣2）
综上所述，满足条件的点P的坐标为：（m， ），（m，2m﹣2）
（3）
解：方法一：
假设在抛物线上存在第一象限内的点Q（x，2x2﹣2），使△BPQ是以P为直角顶点的等腰直角三角形．
如图，过点Q作QE⊥l于点E．
∵∠DBP+∠BPD=90°，∠QPE+∠BPD=90°，
∴∠DBP=∠QPE．
在△DBP与△EPQ中，
，
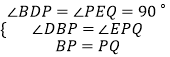∴△DBP≌△EPQ，
∴BD=PE，DP=EQ．
分两种情况：
①当P（m， ）时，
∵B（1，0），D（m，0），E（m，2x2﹣2），
∴ 
，
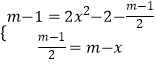解得 
， 
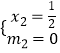（均不合题意舍去）；
②当P（m，2（m﹣1））时，
∵B（1，0），D（m，0），E（m，2x2﹣2），
∴ 
，
解得 ， 
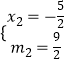（均不合题意舍去）；
综上所述，不存在满足条件的点Q．
方法二：
若在第一象限内存在点Q，
①∵B（1，0），P（m， ），
点Q可视为点B绕点P顺时针旋转90°而成，
将点P平移至原点，得P′（0，0），则点B′（1﹣m， ），
将点B′顺时针旋转90°，则点Q′（ ，m﹣1），
将点P′平移回P（m， ），则点Q′平移后即为点Q，
∴Q（ 
， 
），
将点Q代入抛物线得：m2﹣m=0，
∴m1=1，m2=0，
∴Q1（1，0），Q2（0，﹣ 
）（均不合题意舍去），
②∵B（1，0），P（m，2m﹣2），
同理可得Q（2﹣m，3m﹣3），
将点Q代入抛物线得：3m﹣3=2（2﹣m）2﹣2，
∴2m2﹣11m+9=0，
∴m1=1，m2= 
，
∴Q1（1，0），Q2（﹣ 
， 
）（均不合题意舍去）
综上所述，不存在满足条件的点Q．
【解析】（1）由于抛物线的顶点C的坐标为（0，﹣2），所以抛物线的对称轴为y轴，且与y轴交点的纵坐标为﹣2，即b=0，c=﹣2，再将A（﹣1，0）代入y=ax2+bx+c，求出a的值，由此确定该抛物线的解析式，然后令y=0，解一元二次方程求出x的值即可得到点B的坐标；（2）设P点坐标为（m，n）．由于∠PDB=∠BOC=90°，则D与O对应，所以当以P、D、B为顶点的三角形与以B、C、O为顶点的三角形相似时，分两种情况讨论：①△OCB∽△DBP；②△OCB∽△DPB．根据相似三角形对应边成比例，得出n与m的关系式，进而可得到点P的坐标；（3）假设在抛物线上存在第一象限内的点Q（x，2x2﹣2），使△BPQ是以P为直角顶点的等腰直角三角形．过点Q作QE⊥l于点E．利用AAS易证△DBP≌△EPQ，得出BD=PE，DP=EQ．再分两种情况讨论：①P（m， ）；②P（m，2（m﹣1））．都根据BD=PE，DP=EQ列出方程组，求出x与m的值，再结合条件x＞0且m＞1即可判断不存在第一象限内的点Q，使△BPQ是以P为直角顶点的等腰直角三角形．
【考点精析】关于本题考查的二次函数的图象和二次函数的性质，需要了解二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能得出正确答案．
