��Ŀ����
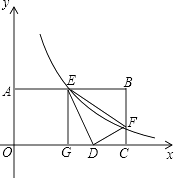
����Ŀ����ͼ����B���߶�AC�ϣ���D��E��ACͬ�࣬��A=��C=90�㣬BD��BE��AD=BC�� 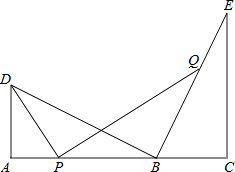
��1����֤��AC=AD+CE��
��2����AD=3��CE=5����PΪ�߶�AB�ϵĶ��㣬����DP����PQ��DP����ֱ��BE�ڵ�Q�� ��i������P��A��B���㲻�غ�ʱ���� ![]() ��ֵ��
��ֵ��
��ii������P��A���˶���AC���е�ʱ�����߶�DQ���е���������·�����߶Σ�������ֱ��д�����������д�������̣�
���𰸡�
��1��֤������BD��BE��
���1+��2=180�㩁90��=90�㣬
�ߡ�C=90�㣬
���2+��E=180�㩁90��=90�㣬
���1=��E��
���ڡ�ABD�͡�CEB�У�
 ��
��
���ABD�ա�CEB��AAS����
��AB=CE��
��AC=AB+BC=AD+CE
��2����i����ͼ������Q��QF��BC��F��
���BFQ�ס�BCE��
�� ![]() ��
��
�� ![]() ��
��
��QF= ![]() BF��
BF��
��DP��PQ��
���APD+��FPQ=180�㩁90��=90�㣬
�ߡ�APD+��ADP=180�㩁90��=90�㣬
���ADP=��FPQ��
�֡ߡ�A=��PFQ=90�㣬
���ADP�ס�FPQ��
�� ![]() ��
��
�� ![]() =
= ![]() ��
��
��5AP��AP2+APBF=3 ![]() BF��
BF��
�������AP��BF����AP��5��=0��
�ߵ�P��A��B���㲻�غϣ�
��AP��5��
��AP=BF��
�ɡ�ADP�ס�FPQ�ã� ![]() =
= ![]() ��
��
�� ![]() =
= ![]() ��
��
��ii���߶�DQ���е���������·�����߶Σ����ǡ�BDQ����λ��MN��
�ɣ�2����i����֪��QF= ![]() AP��
AP��
����P�˶���AC�е�ʱ��AP=4����QF= ![]() ��
��
��BF=QF�� ![]() =4��
=4��
��Rt��BFQ�У����ݹ��ɶ����ã�BQ= ![]() =
= ![]() =
= ![]() ��
��
��MN= ![]() BQ=
BQ= ![]() ��
��
���߶�DQ���е���������·�����߶Σ���Ϊ ![]() ��
��


����������1������ͬ�ǵ������������1=��E�������á��ǽDZߡ�֤����ABD�͡�CBȫ�ȣ�����ȫ�������ζ�Ӧ����ȿɵ�AB=CE��Ȼ�����AC=AB+BC�������ɵ�֤����2����i������Q��QF��BC��F�����ݡ�BFQ�͡�BCE���ƿɵ� ![]() ��Ȼ�����QF=
��Ȼ�����QF= ![]() BF���ٸ��ݡ�ADP�͡�FPQ���ƿɵ�
BF���ٸ��ݡ�ADP�͡�FPQ���ƿɵ� ![]() =
= ![]() ��Ȼ�������õ���AP��BF����5��AP��=0���Ӷ����AP=BF������������������ζ�Ӧ�߳ɱ����ɵ�
��Ȼ�������õ���AP��BF����5��AP��=0���Ӷ����AP=BF������������������ζ�Ӧ�߳ɱ����ɵ� ![]() =
= ![]() ���Ӷ��ý⣻��ii���жϳ�DQ���е��·��Ϊ��BDQ����λ��MN�����QF��BF�ij��ȣ����ù��ɶ������BQ�ij��ȣ��ٸ�����λ���������MN�ij��ȣ�������֮·������
���Ӷ��ý⣻��ii���жϳ�DQ���е��·��Ϊ��BDQ����λ��MN�����QF��BF�ij��ȣ����ù��ɶ������BQ�ij��ȣ��ٸ�����λ���������MN�ij��ȣ�������֮·������
�����㾫����ͨ������������������ε��ж������ʣ��������������ε�һ�ж�Ӧ�߶�(��Ӧ�ߡ���Ӧ���ߡ���Ӧ��ƽ���ߡ����Բ�뾶������Բ�뾶�ȣ��ıȵ������Ʊȣ������������ܳ��ıȵ������Ʊȣ���������������ıȵ������Ʊȵ�ƽ�������Խ����⣮

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�