题目内容
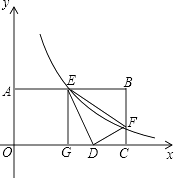
【题目】如图,已知双曲线y= ![]() (k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= .
(k>0)经过Rt△OAB的直角边AB的中点C,与斜边OB相交于点D,若OD=1,则BD= . 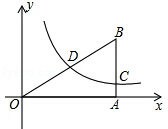
【答案】![]() ﹣1
﹣1
【解析】解:设D的坐标为(a,b),BD=x 过D作DE⊥AO于E,则OE=a,DE=b
由DE∥BA可得,△OED∽△OAB
∴ ![]() ,即
,即 ![]()
∴AO=a+ax,AB=b+bx
∴B(a+ax,b+bx)
又∵点C为AB的中点
∴C(a+ax, ![]() b+
b+ ![]() bx)
bx)
∵点C、D都在反比例函数y= ![]() 的图象上
的图象上
∴k=a×b=(a+ax)×( ![]() b+
b+ ![]() bx)
bx)
整理得,(1+x)2=2
解得x= ![]() ﹣1
﹣1
∴BD的长为: ![]() ﹣1
﹣1
所以答案是: ![]() ﹣1
﹣1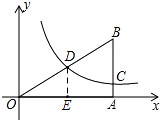
【考点精析】根据题目的已知条件,利用反比例函数的概念和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握形如y=k/x(k为常数,k≠0)的函数称为反比例函数.自变量x的取值范围是x不等于0的一切实数,函数的取值范围也是一切非零实数;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目