Question

【题目】已知抛物线y=-x2-mx+2m2（m＜0）与x轴交于A，B两点，且点A在点B的左侧．

（1）求证：OB=2OA；

（2）若直线y=-x+2与抛物线只有一个公共点，求m的值．

（3）若点C与点O关于点A对称，且以点C为圆心，CO为半径的圆交抛物线于点D，求证：DO平分∠ADB．

Answer 1

【答案】（1）见解析；（2）当时，直线y=-x+2与抛物线只有一个公共点；（3）见解析.

【解析】

（1）令y=0，代入y=-x2-mx+2m2，求出A(m，0)，B(-2m，0)，进而得OB=2OA；

（2）联立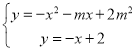，得x2+（m-1）x+（2-2m2）=0，结合直线y=-x+2与抛物线只有一个公共点，得△=0，进而即可求解；

（3）以点C为圆心，CO为半径的圆交抛物线于点D，交点有两个，分两种情况：①当D在x轴上方时，②当D在x轴下方时，分别求证，即可．

（1）∵抛物线y=-x2-mx+2m2（m＜0）与x轴交于A、B两点，

∴关于x的方程-x2-mx+2m2=0有两个不相等的实数根x1和x2，

解得：x1=m，x2=-2m，

∵点A在点B的左边，且m＜0，

∴A(m，0)，B(-2m，0)，

∴OA=-m，OB=-2m，

∴OB=2OA；

（2）∵直线y=-x+2与抛物线只有一个公共点，

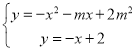∴只有一组实数解，消y得：x2+（m-1）x+（2-2m2）=0，

∴△=0，即（m-1）2-4×1×（2-2m2）=0，

整理得：9m2-2m-7=0，

解得：m1=1（不合题意舍去），．

∴当时，直线y=-x+2与抛物线只有一个公共点；

（3）以点C为圆心，CO为半径的圆交抛物线于点D，交点有两个，

∴CO=CD，

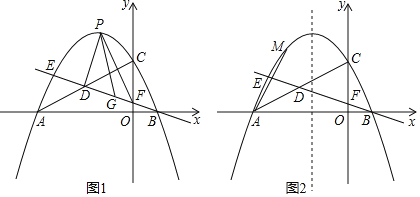
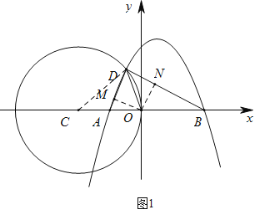
①当D在x轴上方时，如图1，连接CD，

∵点C与点O关于点A对称，

∴OC=2OA=2AC，

又由（1）得OB=2OA，

∴BC=2OC，

∴=，

∵∠DCA=∠BCD，

∴△DCA∽△BCD，

∴BD=2AD，

∵OB=2OA，

∴S△BOD=2S△AOD，

过O点分别作△BOD、△AOD的高ON，OM，

∴S△BOD=，S△AOD=

∴BDON=2ADOM，

∴ON=OM，

∴OD是∠ADB的平分线，即DO平分∠ADB；

②当D在x轴下方时，如图2，

同理①，可得DO平分∠ADB．