题目内容
【题目】如图,已知△ABC.按如下步骤作图:①以A为圆心,AB长为半径画弧;②以C为圆心,CB长为半径画弧,两弧相交于点D;③连结BD,与AC交于点E,连结AD,CD
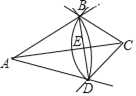
(1)求证:△ABC≌△ADC;
(2)若∠BAC=30°,∠BCA=45°,BC=2;
①求∠BAD所对的弧BD的长;②直接写出AC的长.
【答案】(1)见解析;(2)①![]() ;②
;②![]() .
.
【解析】
(1)由“SSS”可证△ABC≌△ADC;
(2)①由题意可得AC垂直平分BD,可得BE=DE,AC⊥BD,由直角三角形的性质可得BE=CE=![]() ,AB=2BE=2
,AB=2BE=2![]() ,AE=
,AE=![]() BE=
BE=![]() ,由等腰三角形的性质可得∠BAD=2∠BAC=60°,由弧长公式可求弧BD的长;
,由等腰三角形的性质可得∠BAD=2∠BAC=60°,由弧长公式可求弧BD的长;
②由AC=AE+CE可求解.
证明:(1)由题意可得AB=AD,BC=CD,
又∵AC=AC
∴△ABC≌△ADC(SSS);
(2)①∵AB=AD,BC=CD
∴AC垂直平分BD
∴BE=DE,AC⊥BD
∵∠BCA=45°,BC=2;
∴BE=CE=![]() ,且∠BAC=30°,AC⊥BD
,且∠BAC=30°,AC⊥BD
∴AB=2BE=2![]() ,AE=
,AE=![]() BE=
BE=![]()
∵AB=AD,AC⊥BD
∴∠BAD=2∠BAC=60°
∴![]()
②∵AC=AE+CE
∴AC=![]()

练习册系列答案
相关题目