题目内容
【题目】在△ABC中,AB=AC,点D为直线BC上一动点(点D不与B、C重合)以AD为边作正方形ADEF,使∠DAF=∠BAC,连接CF.
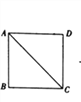
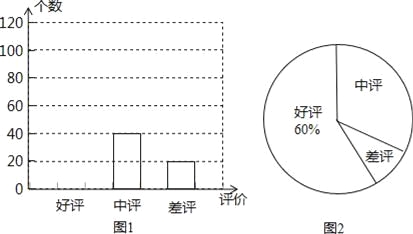
(1)如图1,当点D在线段BC上时,求证:BD=CF;
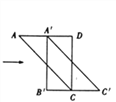
(2)如图2,当点D在线段BC的延长线上,且∠BAC=90°时.
①问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
②延长BA交CF于点G,连接GE,若AB=2![]() ,CD=BC,请求出GE的长.
,CD=BC,请求出GE的长.

【答案】(1)证明见解析;(2)①成立,证明见解析;②GE=2![]() .
.
【解析】试题分析:(1)由SAS证明△DAB≌△FAC,得出对应边相等即可;
(2)①由SAS证明△DAB≌△FAC,得出对应边相等即可;
②过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,证出∠ADH=∠DEM,由AAS证明△ADH≌△DEM,得出EM=DH=6,DM=AH=2,得出CN=EM=6,EN=CM=6,证出△BCG是等腰直角三角形,得出CG=BC=4,求出GN=2,由勾股定理求出GE的长即可.
(1)证明:菱形ADEF中,AD=AF,
∵∠BAC=∠DAF,
∴∠BAD=∠CAF,
在△DAB与△FAC中, 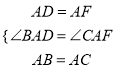 ,
,
∴△DAB≌△FAC(SAS),
∴BD=CF;
(2)解:①(1)中的结论仍然成立;理由如下:
∵∠BAC=∠DAF=90°,
∴∠BAD=∠CAF
在△DAB与△FAC中, 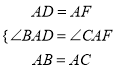 ,
,
∴△DAB≌△FAC(SAS),
∴BD=CF;
②过A作AH⊥BC于H,过E作EM⊥BD于M,EN⊥CF于N,如图所示:
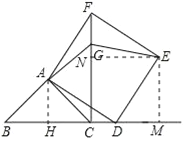
∵∠BAC=90°,AB=AC,
∴BC=![]() AB=4,AH=BH=HC=2,
AB=4,AH=BH=HC=2,
∴CD=BC=4,
∴DH=6,CF=BD=8,
∵四边形ADEF是正方形,
∴AD=DE,∠ADE=90°,
∵BC⊥CF,EM⊥BD,EN⊥CF,
∴四边形CMEN是矩形,
∴NE=CM,EM=CN,
∵∠AHD=∠ADE=∠EMD=90°,
∴∠ADH+∠EDM=∠EDM+∠DEM=90°,
∴∠ADH=∠DEM,
在△ADH与△DEM中, 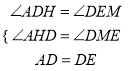 ,
,
∴△ADH≌△DEM(AAS),
∴EM=DH=6,DM=AH=2,
∴CN=EM=6,EN=CM=6,
∵∠ABC=45°,
∴∠BGC=45°,
∴△BCG是等腰直角三角形,
∴CG=BC=4,
∴GN=2,
∴GE=![]() =
=![]() =2
=2![]() .
.

 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案 品学双优卷系列答案
品学双优卷系列答案