题目内容
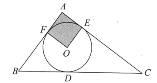
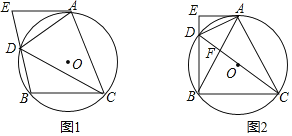
【题目】如图，四边形ADBC内接于⊙O，AD平分∠EDC，AE∥BC交直线BD于E．
（1）求证：AE是⊙O的切线；
（2）若CD为直径，tan∠ADE=2，求sin∠BDC的值．
【答案】（1）见解析（2）
．
【解析】
（1）连接AB，连接AO并延长交BC于F，由圆内接四边形的性质得出∠ADE=∠ACB，再由圆周角定理证出∠ABC=∠ACB，得出AB=AC，得出AF⊥BC，证出AE⊥AF即可得出结论；
（2）连接AO并延长交BC于G，由圆周角定理得出∠DAC=∠CBD=90°，证出四边形AEBG是矩形，得出BG=AE，AG=BE，由三角函数得出AE=2DE，AC=2AD，AG=2CG=BC=2AE=4DE，得出AD=
DE，CD=AD=5DE，即可得出结果．
（1）证明：连接AB，连接AO并延长交BC于F，如图1所示：
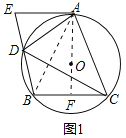
∵四边形ADBC内接于⊙O，AD平分∠EDC，
∴∠ADE=∠ACB，∠ADE=∠ADC，
∵∠ADC=∠ABC，
∴∠ABC=∠ACB，
∴AB=AC，
∴AF⊥BC
∵AE∥BC，
∴AE⊥AF，
∴AE是⊙O的切线；
（2）解：连接AO并延长交BC于G，如图2所示：
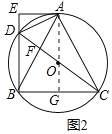
∵CD为直径，
∴∠DAC=∠CBD=90°，
∵AE∥BC，
∴∠E+∠CBD=90°，
∴∠E=90°，
∴四边形AEBG是矩形，
∴BG=AE，AG=BE，
∵∠ADE=∠ADC=∠ACB，
∴
，
∴AE=2DE，AC=2AD，AG=2CG=BC=2AE=4DE，
∴AD=DE，CD=AD=5DE，
∴
．
巧学巧练系列答案
【题目】网上学习越来越受到学生的喜爱．某校信息小组为了解七年级学生网上学习的情况，从该校七年级随机抽取20名学生，进行了每周网上学习的调查．数据如下（单位：时）：
3 | 2.5 | 0.6 | 1.5 | 1 | 2 | 2 | 3.3 | 2.5 | 1.8 |
2.5 | 2.2 | 3.5 | 4 | 1.5 | 2.5 | 3.1 | 2.8 | 3.3 | 2.4 |
整理上面的数据，得到表格如下：
网上学习时间 |
|
|
|
|
人数 | 2 | 5 | 8 | 5 |
样本数据的平均数、中位数、众数如下表所示：
统计量 | 平均数 | 中位数 | 众数 |
数值 | 2.4 |
|
|
根据以上信息，解答下列问题：
（1）上表中的中位数
的值为 ，众数
的值为 ．
（2）用样本中的平均数估计该校七年级学生平均每人一学期（按18周计算）网上学习的时间．
（3）已知该校七年级学生有200名，估计每周网上学习时间超过2小时的学生人数．
