题目内容
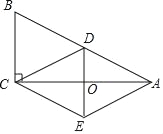
【题目】如图,抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),交y轴于点C,顶点是D.
(1)求抛物线的表达式和顶点D的坐标;
(2)在x轴上取点F,在抛物线上取点E,使以点C、D、E、F为顶点的四边形是平行四边形,求点E的坐标;
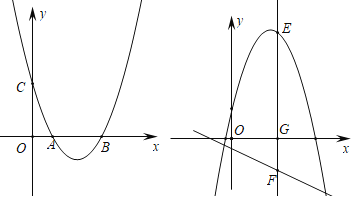
(3)将此抛物线沿着过点(0,2)且垂直于y轴的直线翻折,E为所得新抛物线x轴上方一动点,过E作x轴的垂线,交x轴于G,交直线l:y=-![]() x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
x-1于点F,以EF为直径作圆在直线l上截得弦MN,求弦MN长度的最大值.
【答案】(1)抛物线的表达式为:y=x2-4x+3;D(2,-1);(2)点E的坐标为(2+![]() ,2)或(2-
,2)或(2-![]() ,2)或(2+
,2)或(2+![]() ,4)或(2-
,4)或(2-![]() ,4);(3)MN的最大值为
,4);(3)MN的最大值为![]() .
.
【解析】
(1)利用待定系数法确定函数解析式;
(2)分当CD为平行四边形的对角线、平行四边形的一条边,两种情况求解即可;
(3)则新抛物线的表达式为:y=-(x-2)2+5=-x2+4x+1.设点E的坐标为(x,-x2+4x+1),则点F(x,-![]() x-1),所以EF=-x2+4x+1-(-
x-1),所以EF=-x2+4x+1-(-![]() x-1)=-x2+
x-1)=-x2+![]() x+2.设直线y=-
x+2.设直线y=-![]() x-1与x轴交于点Q.通过锐角三角函数定义得到MN=EFcos∠QFG=
x-1与x轴交于点Q.通过锐角三角函数定义得到MN=EFcos∠QFG=![]() (-x2+
(-x2+![]() x+2),利用配方法求得该函数值的最大值.
x+2),利用配方法求得该函数值的最大值.
解:(1)∵抛物线y=ax2+bx+3的图象经过点A(1,0),B(3,0),
∴![]() .
.
解得![]() .
.
抛物线的表达式为:y=x2-4x+3;
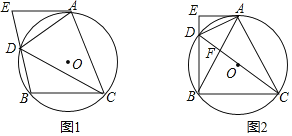
(2)如图1,当CD为平行四边形的对角线时,

设点E的坐标为(x,x2-4x+3),
则CD中点的坐标为(1,1),该点也为EF的中点.
即:x2-4x+3=2×1,解得:x=2±![]() ,
,
E的坐标为(2+![]() ,2)或(2-
,2)或(2-![]() ,2);
,2);

设点F坐标为(m,0),
点D向左平移2个单位、向上平移4个单位,得到点C,
同样点F向左平移2个单位、向上平移4个单位,得到点E(m-2,4),
将点E坐标代入二次函数表达式并解得:m=4±![]() ,
,
则点E(2+![]() ,4)或(2-
,4)或(2-![]() ,4);
,4);
故点E的坐标为(2+![]() ,2)或(2-
,2)或(2-![]() ,2)或(2+
,2)或(2+![]() ,4)或(2-
,4)或(2-![]() ,4);
,4);
(3)抛物线沿着过点(0,2)且垂直与y轴的直线翻折后,顶点坐标为(2,5),
则新抛物线的表达式为:y=-(x-2)2+5=-x2+4x+1.
设点E的坐标为(x,-x2+4x+1),则点F(x,-![]() x-1),
x-1),
EF=-x2+4x+1-(-![]() x-1)=-x2+
x-1)=-x2+![]() x+2.
x+2.
设直线y=-![]() x-1与x轴交于点Q.
x-1与x轴交于点Q.
MN=EFcos∠QFG=![]() (-x2+
(-x2+![]() x+2)=-
x+2)=-![]() (x-
(x-![]() )2+
)2+![]() .
.
由二次函数性质可知,MN的最大值为![]() .
.

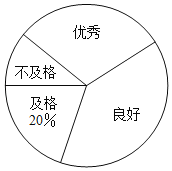
【题目】某校为了解八年级男生“立定跳远”成绩的情况,随机选取该年级部分男生进行测试,以下是根据测试成绩绘制的统计图表的一部分.
成绩等级 | 频数(人) | 频率 |
优秀 | 15 | 0.3 |
良好 | ||
及格 | ||
不及格 | 5 |
根据以上信息,解答下列问题
(1)被测试男生中,成绩等级为“优秀”的男生人数为 人,成绩等级为“及格”的男生人数占被测试男生总人数的百分比为 %;
(2)被测试男生的总人数为 人,成绩等级为“不及格”的男生人数占被测试男生总人数的百分比为 %;
(3)若该校八年级共有180名男生,根据调查结果,估计该校八年级男生成绩等级为“良好”的学生人数.