题目内容
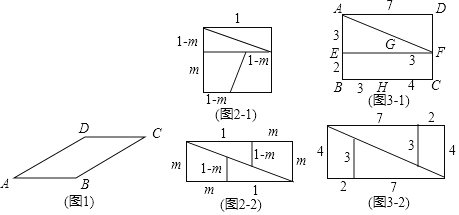
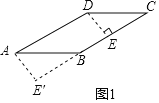
【题目】（1）如图1，在平行四边形ABCD中，∠A＝30°，AB＝6，AD＝8，将平行四边形ABCD分割成两部分，然后拼成一个矩形，请画出拼成的矩形，并说明矩形的长和宽．（保留分割线的痕迹）
（2）若将一边长为1的正方形按如图2﹣1所示剪开，恰好能拼成如图2﹣2所示的矩形，则m的值是多少？
（3）四边形ABCD是一个长为7，宽为5的矩形（面积为35），若把它按如图3﹣1所示的方式剪开，分成四部分，重新拼成如图3﹣2所示的图形，得到一个长为9，宽为4的矩形（面积为36）．问：重新拼成的图形的面积为什么会增加？请说明理由．
【答案】（1）如图所示，见解析；（2）m的值为
；（3）重新拼成的图形的面积会增加，理由见解析．
【解析】
（1）过D作DE⊥BC于E，将△CDE进行平移即可求解；
（2）根据相似三角形的性质即可求解；
（3）根据相似三角形的性质即可求解．
（1）如图所示：
（2）依题意有：
，
解得：
(负值舍去)，
经检验，
是原方程的解.
故m的值为
；
（3）∵
，
∴直角三角形的斜边与直角梯形的斜腰不在一条直线上，
故重新拼成的图形的面积会增加．
练习册系列答案
相关题目
