题目内容
【题目】为了提高学生的汉字书写能力，某学校连续举办了几届汉字听写大赛，今年经过层层选拔，确定了参加决赛的选手，决赛的比赛规则是每正确听写出1个汉字得2分，满分是100分，下面是根据决赛的成绩绘制出的不完整的频数分布表、扇形统计图和频数分布直方图．
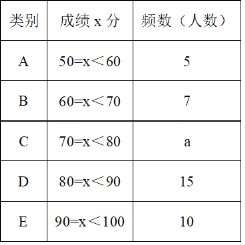
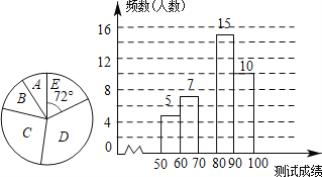
请结合图表完成下列各题
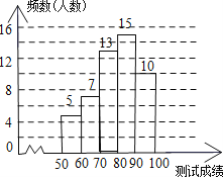
（1）表中a的值为______，并把频数分布直方图补充完整；
（2）学校想利用频数分布表估计这次决赛的平均成绩，请你直接写出平均成绩；
（3）通过与去年的决赛成绩进行比较，发现今年各类人数的中位数有了显著提高，提高了15%以上，求去年各类人数的中位数最高可能是多少？
（4）想从A类学生的3名女生和2名男生中选出两人进行培训，直接写出选中1名男生和1名女生的概率是多少．
【答案】（1）13，补全频数分布直方图见解析；（2）平均成绩为78.6；（3）去年各类人数的中位数最高可能是8；（4）选中1名男生和1名女生的概率
．
【解析】
（1）用E点的频数除以该组的频率得到调查的总人数，然后计算a的值，最后补全频数分布直方图；
（2）取组中值表示各组的平均数，然后根据加权平均数的计算方法求解；
（3）根据中位数的定义得到今年各类人数的中位数为10，然后计算10÷(1+15%)≈8.7，利用人数为整数确定去年各类人数的中位数最高；
（4）画树状图展示所有20种等可能的结果数，找出选中1名男生和1名女生的结果数，然后根据概率公式求解．
（1）调查的总人数为：10÷
=50，
所以
；
故答案为：13；
频数分布直方图为：
（2）平均成绩=
(5×55+7×65+13×75+15×85+10×95)=78.6；
（3）今年各类人数的中位数为10，
10÷(1+15%)≈8.7，
而人数为整数，今年各类人数的中位数比去年提高了15%以上，
去年各类人数的中位数最高可能是：8；
（4）画树状图为：
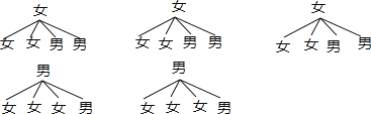
共有20种等可能的结果数，其中选中1名男生和1名女生的结果数为12，
所以选中1名男生和1名女生的概率=
=．
