题目内容
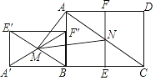
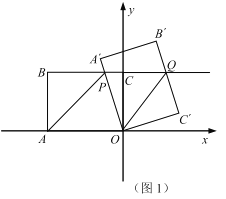
【题目】如图1,![]() 为坐标原点,矩形
为坐标原点,矩形![]() 的顶点
的顶点![]() ,
,![]() ,将矩形
,将矩形![]() 绕点
绕点![]() 按顺时针方向旋转一定的角度
按顺时针方向旋转一定的角度![]() 得到矩形
得到矩形![]() ,此时边
,此时边![]() 、直线
、直线![]() 分别与直线
分别与直线![]() 交于点
交于点![]() 、
、![]() .
.
(1)连接![]() ,在旋转过程中,当
,在旋转过程中,当![]() 时,求点
时,求点![]() 坐标.
坐标.
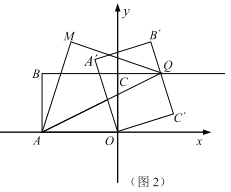
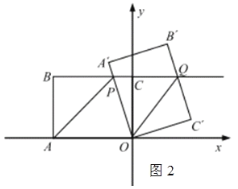
(2)连接![]() ,当
,当![]() 时,若
时,若![]() 为线段
为线段![]() 中点,求
中点,求![]() 的面积.
的面积.
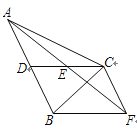
(3)如图2,连接![]() ,以
,以![]() 为斜边向上作等腰直角
为斜边向上作等腰直角![]() ,请直接写出在旋转过程中
,请直接写出在旋转过程中![]() 的最小值.
的最小值.
【答案】(1)P(﹣4,6);(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用∠PAO=∠POA得出PA=PO,进而得出AE=EO=4,即可得出P点坐标;
(2)首先得出Rt△OCQ≌Rt△OC'Q(HL),进而利用平行线的性质求出∠POQ=∠PQO,即可得出BP=PO,再利用勾股定理得出PQ的长,进而求出△OPQ的面积;
(3)先构造一组手拉手的相似三角形,将CM的长转化为![]() ,然后通过垂线段最短及全等三角形求解即可.
,然后通过垂线段最短及全等三角形求解即可.
解:如图1,过点P作PE⊥AO于点E,
∵![]() ,
,
∴AO=8,
∵∠PAO=∠POA
∴PA=PO,
∵PE⊥AO,
∴AE=EO=4,
∴P(﹣4,6);

(2)如图2,在Rt△OCQ和Rt△OC'Q中,
![]() ,
,
∴Rt△OCQ≌Rt△OC'Q(HL),
∴∠OQC=∠OQC',
又∵OP∥C'Q,
∵∠POQ=∠OQC',
∴∠POQ=∠PQO,
∴PO=PQ,
∵点P为BQ的中点,
∴BP=QP,
∴设BP=OP=x,
在Rt△OPC中,OP 2=PC 2+ OC 2,
∴x2=(8﹣x)2+62,
解得:x=![]() .
.
故S△OPQ=![]() ×CO×PQ=
×CO×PQ=![]() ×6×
×6×![]() =
=![]() .
.
(3)如图3,连接CM、AC,在AC的右侧以AC为腰,∠ACG为直角作等腰直角三角形ACG,连接QG,

∵△AMQ与△ACG为等腰直角三角形,
∴![]() ,∠MAQ=∠CAG=45°,
,∠MAQ=∠CAG=45°,
∴![]() ,∠MAC=∠QAG
,∠MAC=∠QAG
∴△MAC∽△QAC,
∴![]() ,
,
∴![]() ,
,
∵点Q在直线BC上,
∴当GQ⊥BC时,GQ取得最小值,
如图3,作GH⊥BC,则GQ的最小值为线段GH的长,
∵∠ACG=∠B=90°,
∴∠ACB+∠GCH=∠ACB+∠BAC=90°,
∴∠GCH=∠BAC,
又∵∠B=∠GHC=90°,AC=CG,
∴△ABC≌△CHG(AAS)
∴GH=BC=8
∴GQ的最小值为8,
∴CM的最小值为![]() .
.