题目内容
【题目】如图,在△ABC中,已知∠ABC=120°,AC=4,

(1)用直尺和圆规作出△ABC的外接圆⊙O(不写作法,保留作图痕迹);
(2)求∠AOC的度数;
(3)求⊙O的半径.
【答案】(1)见解析 (2)120°; (3)![]() .
.
【解析】(1)分别作线段AB于BC的垂直平分线相交于点O,以点O为圆心,OA的长为半径画圆即可;
(2)在优弧AC上取点P,连接AP,PC,利用圆内接四边形的性质求出∠P的度数,再由圆周角定理即可得出∠AOC的度数;
(3)过点O作OD⊥AC于点D,利用垂径定理得出AD的长,根据直角三角形的性质即可得出OA的长.
解:(1)如图,⊙O即为所求;
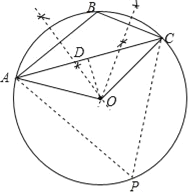
(2)在优弧AC上取点P,连接AP,PC,
∵∠ABC=120°,
∴∠P=180°﹣120°=60°,
∴∠AOC=2∠P=120°;
(3)过点O作OD⊥AC于点D,
∵AC=4,
∴AD=![]() AC=2.
AC=2.
∵∠AOC=120°,OA=OC.
∴∠OAC=![]() =30°,
=30°,
∴OA=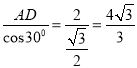 .
.

练习册系列答案
相关题目

