题目内容
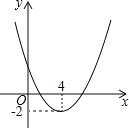
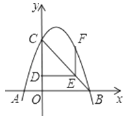
【题目】如图所示,抛物线y=ax2+bx+c(a≠0)经过A(﹣1,0)、B(3,0)、C(0,3)三点.点D从C出发,沿线段CO以1个单位/秒的速度向终点O运动,过点D作OC的垂线交BC于点E,作EF∥OC,交抛物线于点F.
(1)求此抛物线的解析式;
(2)小明在探究点D运动时发现,①当点D与点C重合时,EF长度可看作O;②当点D与点O重合时,EF长度也可以看作O,于是他猜想:设点D运动到OC中点位置时,当线段EF最长,你认为他猜想是否正确,为什么?
(3)连接CF、DF,请直接写出△CDF为等腰三角形时所有t的值.
【答案】(1)y=﹣x2+2x+3(2)点D为OC的中点时,线段EF最长(3)当t=2或![]() 或3时,△CDF为等腰三角形
或3时,△CDF为等腰三角形
【解析】
(1)由于已知抛物线与x轴交点坐标,则设交点式y=a(x+1)(x-3),然后把C点坐标代入求出a即可得到抛物线解析式;
(2)先利用待定系数法求出直线BC的解析式,再设E(t,-t+3),接着表示出D(0,-t+3),F(t,-t2+2t+3),然后用t表示出EF的长,再利用二次函数的性质确定EF最大时的t的值,从而判断点D是否为OC的中点;
(3)先由C(0,3),D(0,-t+3),F(t,-t2+2t+3)和利用两点间的距离公式表示出CD2,CF2,DF2,然后分类讨论:当CD=CF或FC=FD或DC=DF时得到关于t的方程,接着分别解关于t的方程即可.
(1)设抛物线的解析式为y=a(x+1)(x﹣3),
把C(0,3)代入得a1(﹣3)=3,解得a=﹣1,
所以抛物线解析式为y=﹣(x+1)(x﹣3),即y=﹣x2+2x+3;
(2)他猜想正确.理由如下:
设直线BC的解析式为y=mx+n,
把C(0,3),B(3,0)代入得 ![]() ,解得
,解得![]() ,则直线BC的解析式为y=﹣x+3,
,则直线BC的解析式为y=﹣x+3,
设E(t,﹣t+3),则D(0,﹣t+3),F(t,﹣t2+2t+3),
所以EF=﹣t2+2t+3﹣(﹣t+3)=﹣t2+3t=﹣(t﹣![]() )2+
)2+![]() ,
,
当t=![]() 时,EF最大,最大值为
时,EF最大,最大值为![]() ,
,
此时D点坐标为(0,![]() ),
),
所以点D为OC的中点时,线段EF最长;
(3)∵C(0,3),D(0,﹣t+3),F(t,﹣t2+2t+3),
∴CD2=(﹣t+3﹣3)2=t2 , CF2=t2+(﹣t2+2t+3﹣3)2=t2+(﹣t2+2t)2 , DF2=t2+(﹣t2+2t+3+t﹣3)2=t2+(﹣t2+3t)2 ,
当CD=CF时,即t2=t2+(﹣t2+2t)2 , 解得t1=0,t2=2;
当FC=FD,即t2+(﹣t2+2t)2=t2+(﹣t2+3t)2 , 解得t1=0,t2=![]() ;
;
当DC=DF时,即t2=t2+(﹣t2+3t)2 , 解得t1=0,t2=3;
综上所述,当t=2或![]() 或3时,△CDF为等腰三角形.
或3时,△CDF为等腰三角形.

【题目】某班同学上学期全部参加了捐款活动,捐款情况如下统计表:
金额(元) | 5 | 10 | 15 | 20 | 25 | 30 |
人数(人) | 8 | 12 | 10 | 6 | 2 | 2 |
(1)求该班学生捐款额的平均数和中位数;
(2)试问捐款额多于15元的学生数是全班人数的百分之几?
(3)已知这笔捐款是按3:5:4的比例分别捐给灾区民众、重病学生、孤老病者三种被资助的对象,问该班捐给重病学生是多少元?