题目内容
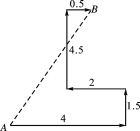
【题目】如图,在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm.点P从点A沿AB方向以1 cm/s的速度运动至点B,点Q从点B沿BC方向以6 cm/s的速度运动至点C,P,Q两点同时出发.
(1)求BC的长;
(2)当点P,Q运动2 s时,求P,Q两点之间的距离;
(3)P,Q两点运动几秒时,AP=CQ?

【答案】(1)BC=24 cm;(2)PQ=13 cm;(3)P,Q两点运动![]() s时,AP=CQ.
s时,AP=CQ.
【解析】
(1)在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm根据勾股定理可得BC2=AC2-AB2=252-72=242,求出BC=24 cm.
(2)连接PQ,由题意知BP=7-2=5(cm),BQ=6×2=12(cm),在Rt△BPQ中,由勾股定理得:
PQ=BP2+BQ2=52+122=132,进而求出PQ=13 cm.
(3)设P,Q两点运动t s时,AP=CQ,则可得t=24-6t,解得t=![]() .
.
解:(1)∵在Rt△ABC中,∠B=90°,AB=7 cm,AC=25 cm
∴BC2=AC2-AB2=252-72=242,
∴BC=24 cm.
(2)连接PQ,
由题意知BP=7-2=5(cm),BQ=6×2=12(cm),
在Rt△BPQ中,由勾股定理,得:
PQ=BP2+BQ2=52+122=132,
∴PQ=13 cm.
(3)设P,Q两点运动t s时,
AP=CQ,则t=24-6t,
解得t=![]() .
.
答:P,Q两点运动![]() s时,AP=CQ.
s时,AP=CQ.

练习册系列答案
相关题目