题目内容
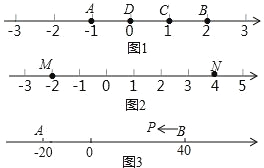
【题目】如果事件A发生的概率是 
，那么在相同条件下重复试验，下列4种陈述中，不正确的有 ①说明做100次这种试验，事件A必发生1次
②说明事件A发生的频率是
③说明做100次这种试验中，前99次事件A没发生，后1次事件A才发生
④说明做100次这种试验，事件A可能发生1次（ ）
A.①、②、③
B.①、②、④
C.②、③、④
D.①、②、③、④
【答案】A
【解析】解：∵事件A发生的概率是 
，并不能说明做100次这种试验，事件A必发生1次，有可能多次，也有可能1次不发生， ∴选项①符合题意；
∵事件A发生的概率是 ，并不能说明事件A发生的频率是 ，
∴选项②符合题意；
∵事件A发生的概率是 ，并不能说明做100次这种试验中，前99次事件A没发生，后1次事件A才发生，
∴选项③符合题意；
∵事件A发生的概率是 ，说明做100次这种试验，事件A可能发生1次，
∴选项④不符合题意，
∴4种陈述中，不正确的有：①、②、③．
故选：A．
【考点精析】利用概率的意义对题目进行判断即可得到答案，需要熟知任何事件的概率是0~1之间的一个确定的数，它度量该事情发生的可能性．小概率事件很少发生，而大概率事件则经常发生．知道随机事件的概率有利于我们作出正确的决策．
【题目】十八世纪瑞士数学家欧拉证明了简单多面体中顶点数（V）、面数（F）、棱数（E）之间存在的一个有趣的关系式，请你观察下列几种简单多面体模型，解答下列问题：
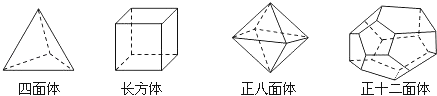
图1 图2
（探索新知）如图1，（1）根据上面多面体模型，完成表格中的空格；
多面体 | 顶点数（V） | 面数（F） | 棱数（E） |
四面体 | 4 | 4 | |
长方体 | 8 | 6 | 12 |
正八面体 | 8 | 12 | |
正十二面体 | 20 | 12 | 30 |
你发现顶点数（V）、面数（F）、棱数（E）之间存在的关系式是 ．
（2）根据以上关系式猜想是否存在一个多面体，它有16个面，50条棱，34个顶点？并写出理由。
（实际应用）如图2，足球一般有32块黑白皮子缝合而成，黑色的是正五边形，白色的是正六边形，如
果我们近似把足球看成一个多面体．
（1）设黑色的正五边形有x块，则白色的正六边形有（32﹣x）块，当把足球看成一个多面体时，它的棱数是 ，它的顶点数是 ．
（2）求出黑皮和白皮各有多少块？
