题目内容
【题目】如图,在等边△ABC中,AD是BC边上的高,∠BDE=∠CDF=30°,在下列结论中:①△ABD≌△ACD;②2DE=2DF=AD;③△ADE≌△ADF;④4BE=4CF=AB.正确的个数是( )

A. 1 B. 2 C. 3 D. 4
【答案】D
【解析】
由等边三角形的性质可得BD=DC,AB=AC,∠B=∠C=60°,利用SAS可证明△ABD≌△ACD,从而可判断①正确;利用ASA可证明△ADE≌△ADF,从而可判断③正确;在Rt△ADE与Rt△ADF中,∠EAD=∠FAD=30°,根据30度角所对的直角边等于斜边的一半可得2DE=2DF=AD,从而可判断②正确;同理可得2BE=2CF=BD,继而可得4BE=4CF=AB,从而可判断④正确,由此即可得答案.
∵等边△ABC中,AD是BC边上的高,
∴BD=DC,AB=AC,∠B=∠C=60°,
在△ABD与△ACD中
 ,
,
∴△ABD≌△ACD,故①正确;
在△ADE与△ADF中
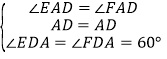 ,
,
∴△ADE≌△ADF,故③正确;
∵在Rt△ADE与Rt△ADF中,
∠EAD=∠FAD=30°,
∴2DE=2DF=AD,故②正确;
同理2BE=2CF=BD,
∵AB=2BD,
∴4BE=4CF=AB,故④正确,
故选D.

练习册系列答案
相关题目




