题目内容
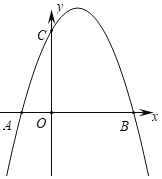
【题目】如图,抛物线L1:y=ax2+bx+c(a≠0)与x轴交于A、B两点,与y轴交于C点,且A(﹣1,0),OB=OC=3OA.若抛物线L2与抛物线L1关于直线x=2对称.
(1)求抛物线L1与抛物线L2的解析式;
(2)在抛物线L1上是否存在一点P,在抛物线L2上是否存在一点Q,使得以BC为边,且以B、C、P、Q为顶点的四边形为平行四边形?若存在,求出P、Q两点的坐标,若不存在,请说明理由.
【答案】(1)抛物线L1的解析式为y=-x2+2x+3,抛物线L2的解析式为y=-(x-3)2+4;(2)存在P(2,3),Q(5,0)或P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
【解析】
(1)用待定系数法求抛物线L1的解析式并配方成顶点式,得到抛物线L1的顶点坐标D;由抛物线L2与抛物线L1关于直线x=2对称可得两抛物线开口方向、大小相同,且两顶点关于直线x=2对称,因此求得抛物线L2的顶点D',进而得到抛物线L2的顶点式;
(2)由于BC为边,以B、C、P、Q为顶点的四边形为平行四边形,所以有两种情况:①BQ∥PC,BQ=PC;②BP∥CQ,BP=CQ.因为可把点B、C之间看作是向左(或右)平移3个单位,再向上(或下)平移3个单位得到,所以点P、Q之间也有相应的平移关系,故可由点P坐标(t,t+2t+3)的t表示点Q坐标,再把点Q坐标代入抛物线L2解方程即求得t的值,进而求得点P、Q坐标.
(1)∵A(﹣1,0),
∴OB=OC=3OA=3,
∴B(3,0),C(0,3)
∵抛物线L1:y=ax2+bx+c经过点A、B、C,
∴ ,解得:
,解得: ,
,
∴抛物线L1的解析式为y=-x2+2x+3=-(x-1)2+4,
∴抛物线L1的顶点D(1,4),
∵抛物线L2与抛物线L1关于直线x=2对称,
∴两抛物线开口方向、大小相同,抛物线L2的顶点D'与点D关于直线x=2对称,
∴D'(3,4),
∴抛物线L2的解析式为y=-(x-3)2+4;
(2)存在满足条件的P、Q,使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形,设抛物线L1上的P(t,-t2+2t+3),
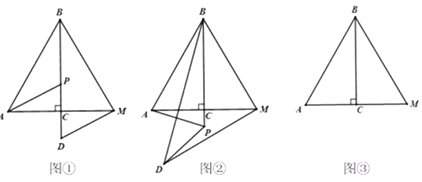
①若四边形BCPQ为平行四边形,如图1,

∴BQ∥PC,BQ=PC,
∴BQ可看作是CP向右平移3个单位,再向下平移3个单位得到的,
∴Q(t+3,-t2+2t),
∵点Q在抛物线L2上,
∴﹣t2+2t=-(t+3-3)2+4,解得:t=2,
∴P(2,3),Q(5,0);
②若四边形BCQP为平行四边形,如图2,
∴
BP∥CQ,BP=CQ,
∴CQ可看作是BP向左平移3个单位,再向上平移3个单位得到的,
∴Q(t﹣3,-t2+2t+6),
∴﹣t2+2t+6=-(t-3-3)2+4,解得:t![]() ,
,
∴P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() );
);
综上所述:存在P(2,3),Q(5,0)或P(![]() ,
,![]() ),Q(
),Q(![]() ,
,![]() ),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.
),使得以BC为边且以B、C、P、Q为顶点的四边形为平行四边形.