题目内容
【题目】如图,![]() 为等边
为等边![]() 的高,
的高,![]() ,点P为直线
,点P为直线![]() 上的动点(不与点B重合),连接
上的动点(不与点B重合),连接![]() ,将线段
,将线段![]() 绕点P逆时针旋转60°,得到线段
绕点P逆时针旋转60°,得到线段![]() ,连接
,连接![]() 、
、![]() .
.
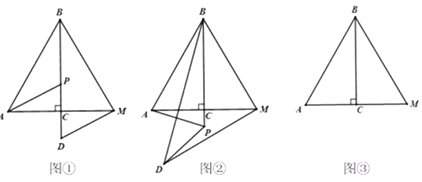
(1)问题发现:如图①,当点D在直线![]() 上时,线段
上时,线段![]() 与
与![]() 的数量关系为_________,
的数量关系为_________,![]() _________;
_________;
(2)拓展探究:如图②,当点P在![]() 的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
的延长线上时,(1)中结论是否成立?若成立,请加以证明;若不成立,请说明理由;
(3)问题解决:当![]() 时,请直接写出线段
时,请直接写出线段![]() 的长度.
的长度.
【答案】(1)相等;90°;(2)成立,证明见解析;(3)4或![]()
【解析】
(1)连接AD,通过SAS证明![]() ,然后对应边、对应角相等、等量减等量,即可得出结论;
,然后对应边、对应角相等、等量减等量,即可得出结论;
(2)连接AD,通过SAS证明![]() ,然后对应边、对应角相等、等量加等量,即可得出结论;
,然后对应边、对应角相等、等量加等量,即可得出结论;
(3)通过前两问,我们知道![]() 是等边三角形,点D的轨迹是AP旋转60°得来的,A为定点,P再BC上运动是主动点,D为从动点,根据瓜豆原理可以得出D的轨迹是一条直线;BM长为定值、
是等边三角形,点D的轨迹是AP旋转60°得来的,A为定点,P再BC上运动是主动点,D为从动点,根据瓜豆原理可以得出D的轨迹是一条直线;BM长为定值、![]() 也为定值,利用定弦定角模型可知点D还应在圆弧上,因为点P可能在B点上方,还可能在C点下方,所以轨迹应为两段圆弧;通过以上分析可以作出图形,找到两种轨迹的交点,确定D点,求出AD即求出AP.
也为定值,利用定弦定角模型可知点D还应在圆弧上,因为点P可能在B点上方,还可能在C点下方,所以轨迹应为两段圆弧;通过以上分析可以作出图形,找到两种轨迹的交点,确定D点,求出AD即求出AP.
解:(1)相等;90°;
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
由旋转的性质可得:![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,![]()
∴![]()
即![]()
在![]() 与
与![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,![]()
∴![]()
(2)成立,证明如下:
如图②,连接![]() ,
,
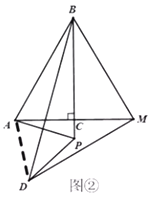
∵![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
由旋转的性质可得:![]() ,
,![]() ,
,
∴![]() 是等边三角形,
是等边三角形,
∴![]() ,
,
∴![]() ,
,
![]() ,
,
![]()
∴![]() ,
,
在![]() 与
与![]() 中,
中,
∵ ,
,
∴![]() ,
,
∴![]() ,
,![]() .
.
∵![]() ,
,
∴![]()
(3)点P在直线BC上运动,由瓜豆原理可知,D点也应在直线上运动,在BC上选取两个特殊的P点位置,按照题意作出对应D点,然后连接点D所在直线确定;因为![]() 所以BM所对圆心角为60°,按照圆心在BM左侧和右侧两种情况,作出点D所在两端圆弧,直线与两端圆弧交点,即满足题意的点D,具体图形如下:
所以BM所对圆心角为60°,按照圆心在BM左侧和右侧两种情况,作出点D所在两端圆弧,直线与两端圆弧交点,即满足题意的点D,具体图形如下:
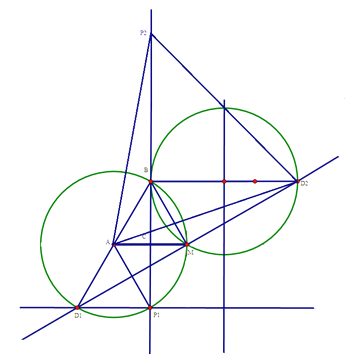
AP1=AD1=4;
AP2=AD2=![]()
综上所述,AP长为4或![]() .
.

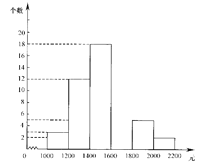
【题目】小明在“五一”假期间参加一项社会调查活动,在他所居住小区的600个家庭中,随机调查了50个家庭人均月收入情况,并绘制了如下的频数分布表和频数分布直方图(收入取整数,单位:元).
分 组 | 频 数 | 频 率 |
1000~1200 | 3 | 0.060 |
1200~1400 | 12 | 0.240 |
1400~1600 | 18 | 0.360 |
1600~1800 | 0.200 | |
1800~2000 | 5 | |
2000~2200 | 2 | 0.040 |
合计 | 50 | 1.000 |
请你根据以上提供的信息,解答下列问题:
⑴ 补全频数分布表和频数分布直方图;
⑵ 这50个家庭人均月收入的中位数落在 小组;
⑶ 请你估算该小区600个家庭中人均月收入较低(不足1400元)的家庭个数大约有多少?