Question

【题目】在平面直角坐标系中,已知点A(4,0),B(2,0),若点C在一次函数y=x+2的图象上,且△ABC为直角三角形,则满足条件的点C有（ ）

A.4个B.2个C.3个D.1个

Answer 1

【答案】A

【解析】

根据已知可求得直线与两轴的交点，①分别过点A、点B作垂线，可得出符合题意的点C，②利用圆周角定理，可得出符合条件的两个点C．

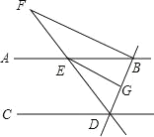
由题意知,直线y=x+2与x轴的交点为(4,0)，与y轴的交点为(0,2)，如图：

过点A作垂线与直线的交点W(4,4)，
过点B作垂线与直线的交点S(2,1)，
过AB中点E(1,0),作垂线与直线的交点为F(1,2.5)，
则EF=2.5<3，
所以以3为半径，以点E为圆心的圆与直线必有两个交点
∴共有四个点能与点A，点B组成直角三角形。
故选A.