题目内容
【题目】(本题满分12分)如图,平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,点P从O沿OB边向点B移动,点Q从点B沿BC边向点C移动,P,Q同时出发,速度都是1cm/s.
(1)求经过O,B,D三点的抛物线的解析式;
(2)判断P,Q移动几秒时,△PBQ为等腰三角形;
(3)若允许P点越过B点在BC上运动,Q点越过C点在CD上运动,设线PQ与OB,BC,DC围成的图形面积为y(cm2),点P,Q的移动时间为t(s),请写出y与t之间的函数关系式,并写出t的取值范围.

【答案】见解析
【解析】解:(1)过点D作DM⊥OB于M,
∵平行四边形OBCD中,OB=8cm,BC=6cm,∠DOB=45°,
∴OD=BC=6cm,
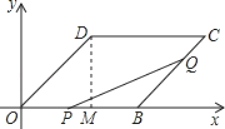
∴OM=DM=ODsin45°=6×![]() =3
=3![]() ,
,
∴D(3![]() ,3
,3![]() ),B(8,0),
),B(8,0),
设经过O,B,D三点的抛物线的解析式为:y=ax(x﹣8),
将D的坐标代入得:3![]() =3
=3![]() a(3
a(3![]() ﹣8),
﹣8),
解得:a=﹣![]() ,∴y=﹣
,∴y=﹣![]() x(x﹣8);
x(x﹣8);
(2)∵∠PBQ=180°﹣∠DOB=135°,
∴若△PBQ为等腰三角形,则PB=BQ.
设P,Q移动t秒时,△PBQ为等腰三角形,
∴P点走过的路程为t,Q点走过的路程为t,
∴PB=OB﹣t=8﹣t(cm),BQ=tcm.若PB=BQ,则8﹣t=t,解得:t=4(s).
∴P,Q移动4秒时,△PBQ为等腰三角形;
(3)如图:过点D作DM⊥OB于M,过点P作PN⊥OB于N,交CD于H,
∵四边形OBCD是平行四边形,
∴CD=OB=8cm,BC=OD=6cm,CD∥OB,HN=DM=3![]() cm,
cm,
∴PH⊥CD,△CPH∽△BPN,
∴![]() ,
,
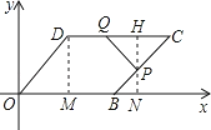
由题意得:PC=14﹣t(cm),PB=t﹣8(cm),CQ=t﹣6(cm),
∴![]() ,
,
解得:PH=![]() (14﹣t),
(14﹣t),
∴y=SOBCD﹣S△CPQ=8×3![]() ﹣
﹣![]() (t﹣6)×
(t﹣6)×(14﹣t)=
![]() t2﹣5
t2﹣5![]() t+45
t+45![]() ,
,
∵P点越过B点在BC上运动,Q点越过C点在CD上运动,
∴8<t≤14,
∴y与t之间的函数关系式为y=![]() t2﹣5
t2﹣5![]() t+45
t+45![]() ,t的取值范围为8<t≤14.
,t的取值范围为8<t≤14.