题目内容
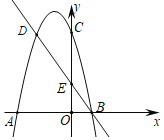
【题目】如图,![]() 中,
中,![]() ,点
,点![]() 位于第一象限,点
位于第一象限,点![]() 为坐标原点,点
为坐标原点,点![]() 在
在![]() 轴正半轴上,若双曲线
轴正半轴上,若双曲线![]()
![]() 与
与![]() 的边
的边![]() 、
、![]() 分别交于点
分别交于点![]() 、
、![]() ,点
,点![]() 为
为![]() 的中点,连接
的中点,连接![]() 、
、![]() .若
.若![]() ,则
,则![]() 为_______________.
为_______________.
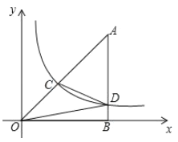
【答案】![]()
【解析】
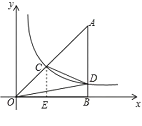
根据反比例函数关系式与面积的关系得S△COE=S△BOD=3,由C是OA的中点得S△ACD=S△COD,由CE∥AB,可知△COE∽△AOB,由面积比是相似比的平方得![]() ,求出△ABC的面积,从而求出△AOD的面积,得出结论.
,求出△ABC的面积,从而求出△AOD的面积,得出结论.
过C作CE⊥OB于E,
∵点C、D在双曲线![]() (x>0)上,
(x>0)上,
∴S△COE=S△BOD,
∵S△OBD=3,
∴S△COE=3,
∵CE∥AB,
∴△COE∽△AOB,
∴![]() ,
,
∵C是OA的中点,
∴OA=2OC,
∴![]() ,
,
∴S△AOB=4×3=12,
∴S△AOD=S△AOBS△BOD=123=9,
∵C是OA的中点,
∴S△ACD=S△COD,
∴S△COD=![]() ,
,
故答案为![]() .
.

练习册系列答案
相关题目
【题目】抛物线![]() 中,函数值y与自变量
中,函数值y与自变量![]() 之间的部分对应关系如下表:
之间的部分对应关系如下表:
| … |
|
|
| 0 | 1 | … |
y | … |
|
| 0 |
|
| … |
(1)求该抛物线的表达式;
(2)如果将该抛物线平移,使它的顶点移到点M(2,4)的位置,那么其平移的方法是____________.