题目内容
【题目】在等腰△ABC中,∠ACB=90°,且AC=1.过点C作直线l∥AB,P为直线l上一点,且AP=AB.则点P到BC所在直线的距离是( )
A.1
B.1或 ![]()
C.1或 ![]()
D.![]() 或
或 ![]()
【答案】D
【解析】解:①如图,延长AC,做PD⊥BC交点为D,PE⊥AC,交点为E,
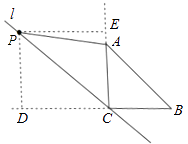
∵CP∥AB,
∴∠PCD=∠CBA=45°,
∴四边形CDPE是正方形,
则CD=DP=PE=EC,
∵在等腰直角△ABC中,AC=BC=1,AB=AP,
∴AB= ![]() =
= ![]() ,
,
∴AP= ![]() ;
;
∴在直角△AEP中,(1+EC)2+EP2=AP2
∴(1+DP)2+DP2=( ![]() )2,
)2,
解DP= ![]() ;
;
②如图,延长BC,作PD⊥BC,交点为D,延长CA,作PE⊥CA于点E,
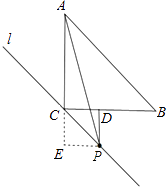
同理可证,四边形CDPE是正方形,
∴CD=DP=PE=EC,
同理可得,在直角△AEP中,(EC﹣1)2+EP2=AP2,
∴(PD﹣1)2+PD2=( ![]() )2,
)2,
解得,PD= ![]() ;
;
所以答案是:D.
【考点精析】通过灵活运用等腰直角三角形和平行线之间的距离,掌握等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;两条平行线的距离:两条直线平行,从一条直线上的任意一点向另一条直线引垂线,垂线段的长度,叫做两条平行线的距离即可以解答此题.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案
相关题目