题目内容
【题目】如图,在等腰直角△ABC中∠ABC=90°,AD平分∠BAC,点M、N分别是AD,AB上一动点,当AC=6时,BM+MN的最小值等于_______。

【答案】3.
【解析】
作N关于AD的对称点为R,作AC边上的高BE(E在AC上),求出BM+MN=BR,根据垂线段最短得出BM+MN≥BE,求出BE即可得出BM+MN的最小值.
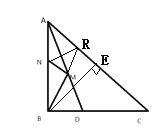
解:作N关于AD的对称点为R,作AC边上的高BE(E在AC上),
∵AD平分∠CAB,
∴R必在AC上,
∵N关于AD的对称点为R,
∴MR=MN,
∴BM+MN=BM+MR,
即BM+MN=BR≥BE(垂线段最短),
∵等腰直角△ABC,∠ABC=90°,BE⊥AC,
∴AE=CE,
∴BE=![]() AC=3.
AC=3.
故答案为:3.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目