题目内容
【题目】如图,在6×8的网格中,每个小正方形的边长均为1,点O和△ABC的顶点均为小正方形的顶点.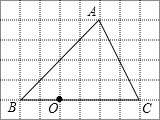
(1)在图中△ABC的内部作△A′B′C′,使△A′B′C′和△ABC位似,且位似中心为点O,位似比为1:2;
(2)连接(1)中的AA′,则线段AA′的长度是 .
【答案】
(1)解:如图,△A′B′C′为所作;
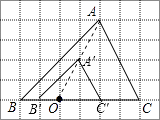
(2)![]()
【解析】解:(1)如图,△A′B′C′为所作;

(2)OA= ![]() =2
=2 ![]() ,
,
∵OA′:OA=1:2,
∴点A′为OA的中点,
∴AA′= ![]() .
.
所以答案是 :(1)见解答过程;(2)![]() .
.
【考点精析】关于本题考查的作图-位似变换,需要了解对应点到位似中心的距离比就是位似比,对应线段的比等于位似比,位似比也有顺序;已知图形的位似图形有两个,在位似中心的两侧各有一个.位似中心,位似比是它的两要素才能得出正确答案.

练习册系列答案
相关题目