��Ŀ����
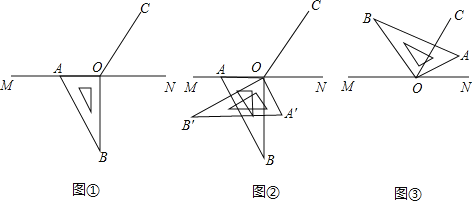
����Ŀ����ͼ�٣���OΪֱ��MN��һ�㣬����O��ֱ��OC��ʹ��NOC=60������һ��ֱ�����dzߵ�ֱ�Ƕ�����ڵ�O����һ��OA������OM�ϣ���һ��OB��ֱ��AB���·������С�OBA=30��
��1����ͼ���е����dz���ֱ��OC��������A��B��O�����A��ON�Ķ�����
��2����ͼ���е����dz��Ƶ�O��ÿ��10�����ٶ���˳ʱ�뷽����ת����ת��Ϊ����0������360����������ת�Ĺ����У��ڵڼ���ʱ��ֱ��OAǡ��ƽ����ǡ�NOC��
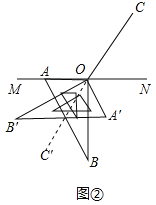
��3����ͼ���е����dz��Ƶ�O˳ʱ����ת������A��B����ֱ��MN�Ϸ�ʱ����ͼ����ʾ������̽����MOB���AOC֮���������ϵ����ֱ��д�����ۣ�����д�����ɣ�
���𰸡���1����A��ON=60������2����15����ʱ��ֱ��OAǡ��ƽ����ǡ�NOC����3���ٵ�OB��OA��OC������ʱ����MOB-��AOC=30�����ڵ�OB��OA��OC��ͬ��ʱ����MOB+��AOC=120��-90��=30����
��������
��1����ͼ���У��ӳ�CO��C�������÷��۲����������A��O��C�����ɽ�����⣻
��2����t��ʱ��ֱ��OAǡ��ƽ����ǡ�NOC���������̼��ɽ�����⣻
��3�����������ηֱ���⼴�ɽ�����⣻
��1����ͼ���У��ӳ�CO��C����
�����dz���ֱ��OC��������A��B��O��
���A��OC��=��AOC��=��CON=60����
���A��ON=180��-60��-60��=60����
��2����t��ʱ��ֱ��OAǡ��ƽ����ǡ�NOC��
������10t=150��10t=330��
���t=15��33s��
�𣺵�15����ʱ��ֱ��OAǡ��ƽ����ǡ�NOC��
��3���ٵ�OB��OA��OC������ʱ���ߡ�AOB=90����
��120��-��MOB+��AOC=90����
���MOB-��AOC=30����
�ڵ�OB��OA��OC��ͬ��ʱ����MOB+��AOC=120��-90��=30����