题目内容
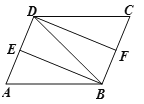
【题目】如图，在平行四边形ABCD中，以点A为圆心，AB长为半径画弧交AD于点F，再分别以点B、F为圆心，大于
长为半径画弧，两弧交于一点P，连接AP并延长交BC于点E，连接EF．
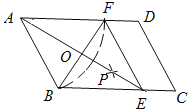
（1）四边形ABEF是_______；（选填矩形、菱形、正方形、无法确定）（直接填写结果）
（2）AE，BF相交于点O，若四边形ABEF的周长为40，BF=10，则AE的长为________，∠ABC=________°．（直接填写结果）
【答案】（1）菱形；（2）AE=10
，∠ABC=120°.
【解析】
试题（1）根据角平分线的画法以及菱形的判定方法得出答案；（2）根据菱形的性质得出AF的长度，然后根据勾股定理得出AE的长度，最后根据∠ABO的正弦值得出角度.
试题解析：（1）菱形
（2）依题意，可知AE为角平分线，因为ABEF的周长为40，所以，AF＝10，
又FO＝5，AO＝
＝
，所以，AE＝
，
，所以，∠ABO＝120°，∠ABC＝120°
练习册系列答案
课堂全解字词句段篇章系列答案
步步高口算题卡系列答案
点睛新教材全能解读系列答案
小学教材完全解读系列答案
相关题目
