题目内容
【题目】在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是线段
是线段![]() 的中点,点
的中点,点![]() 在射线
在射线![]() 上,连接
上,连接![]() ,平移
,平移![]() ,使点
,使点![]() 移动到点
移动到点![]() ,得到
,得到![]() (点
(点![]() 与点
与点![]() 对应,点
对应,点![]() 与点
与点![]() 对应),
对应),![]() 交
交![]() 于点
于点![]() .
.
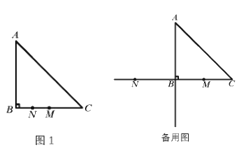
(1)若点![]() 是线段
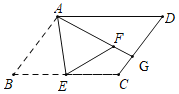
是线段![]() 的中点,如图1.
的中点,如图1.
①依题意补全图1;
②求![]() 的长;
的长;
(2)若点![]() 在线段
在线段![]() 的延长线上,射线
的延长线上,射线![]() 与射线
与射线![]() 交于点
交于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)①见解析;②![]() ;(2)CE=
;(2)CE=![]()
【解析】
(1)①利用平移的性质画出图形;
②利用相似得出比例,即可求出线段DP的长.
(2)根据条件MQ=DP,利用平行四边形的性质和相似三角形的性质,求出BN的长即可解决.
解:(1)①如图1,补全图形
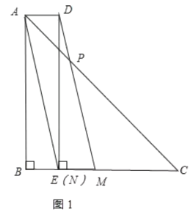
②连接AD,如图1.
在Rt△ABN中,
∵∠B=90°,AB=4,BN=1,
∴AN=![]() ,
,
∵线段AN平移得到线段DM,
∴DM=AN=![]() ,
,
AD=NM=1,AD∥MC,
∴△ADP∽△CMP.
∴![]() ,
,
∴![]() ;
;
(2)如图,连接NQ,
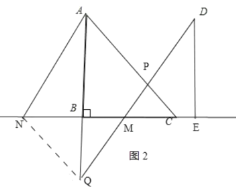
由平移知:AN∥DM,且AN=DM.
∵MQ=DP,
∴PQ=DM.
∴AN∥PQ,且AN=PQ.
∴四边形ANQP是平行四边形.
∴NQ∥AP.
∴∠BQN=∠BAC=45°.
又∵∠NBQ=∠ABC=90°,
∴BN=BQ.
∵AN∥MQ,
∴![]() ,
,
又∵M是BC的中点,且AB=BC=4,
∴![]() ,
,
∴NB=![]() 或
或![]() (负数舍去).
(负数舍去).
∴ME=BN=![]() .
.
∴CE=![]()

练习册系列答案
相关题目
【题目】为了解八年级学生双休日的课外阅读情况,学校随机调查了该年级25名学生,得到了一组样本数据,其统计表如下:
八年级25名学生双休日课外阅读时间统计表
阅读时间 | 1小时 | 2小时 | 3小时 | 4小时 | 5小时 | 6小时 |
人数 | 3 | 4 | 6 | 3 | 2 |
(1)请求出阅读时间为4小时的人数所占百分比;
(2)试确定这个样本的众数和平均数.