��Ŀ����
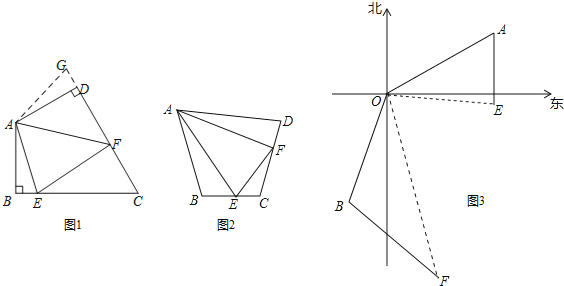
����Ŀ�������ⱳ������ͼ1�����ı���ABCD�У�AB��AD����BAD��120�㣬��B����ADC��90�㣬�ҡ�EAF��60�㣬̽��ͼ���߶�BE��EF��FD֮���������ϵ��С��ͬѧ�ķ����ǽ���ABE�Ƶ�A��ʱ����ת120�㵽��ADG��λ�ã�Ȼ����֤����AFE �ա�AFG���Ӷ��ó�ʲô������
��̽�����죩��ͼ2�������ı���ABCD�У�AB��AD����B����D��180�㣬E��F�ֱ���BC��CD�ϵĵ㣬�ҡ�EAF��![]() ��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
��BAD�����������Ƿ���Ȼ��������˵�����ɣ�
������Ӧ�ã���ͼ3����ij�ξ�����ϰ�У���ͧ����ָ�����ģ�O������ƫ��60���A������ͧ����ָ��������ƫ��20���B������������ͧ��ָ�����ĵľ�����ȣ��ӵ��ж�ָ���ͧ�������Ϸ�����30����/Сʱ���ٶ�ǰ������ͧ������ƫ��40��ķ�����50����/Сʱ���ٶ�ǰ����1Сʱ��ָ�����Ĺ۲�ס�������ͧ�ֱ�E��F����������ͧ��ָ������O֮��нǡ�EOF��70�㣬�����ʱ����֮ͧ��ľ��룮
���𰸡�(1) ![]() (2)
(2) ![]() (3) ��ʱ����֮ͧ��ľ���Ϊ180���
(3) ��ʱ����֮ͧ��ľ���Ϊ180���
��������
�������ⱳ��������ABE�Ƶ�A��ʱ����ת120������ADG��λ�ú�AE=AG��DG=BE����EAF����FAG=60��������SAS֤����AFE �ա�AFG���ɵó����ۣ�̽�����죺�ӳ�FD����G��ʹDG��BE������AG��ͨ��SAS��֤����ABE�ա�ADG����AE��AG����BAE����DAG����EAF����FAG=60����������AEF�ա�AGF��EF=FG������FG��DG��DF��BE��DF����EF��BE��FD��Ȼ����������Ӧ�ã�����EF���ߡ�AOB��140������FOE��70����![]() ��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪAE=80��FB=100�����������ʱ����֮ͧ��ľ���EF��
��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪAE=80��FB=100�����������ʱ����֮ͧ��ľ���EF��
������������ⱳ��������ABE�Ƶ�A��ʱ����ת120������ADG��λ�ú�AE=AG��DG=BE����BAE����DAG����EAF��60������EAG��120����������FAG=60������EAG����FAG��������AFE �ա�AFG��SAS���� ��EF=FG����FG��DG��DF������EF��BE��FD��̽�����죺EF��BE��FD��Ȼ�������ӳ�FD����G��ʹDG��BE������AG����ΪAB=AD����B����ADG��90����������ABE�ա�ADG������ ��AE��AG����BAE����DAG��������EAG����FAG=60����������AEF�ա�AGF��SAS������EF=FG������FG��DG��DF��BE��DF����EF��BE��FD������Ӧ�ã�����EF���ߡ�AOB��30����90����20����140������FOE��70����![]() ��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪBF=50��2=100��AE=40��2=80�� ���Դ�ʱ����֮ͧ��ľ���EF��AE��FB=80+100=180�������ʱ����֮ͧ��ľ���Ϊ180���
��AOB������OA��OB����A����B��60����120����180��������̽�������е�������������EF��AE��FB��������ΪBF=50��2=100��AE=40��2=80�� ���Դ�ʱ����֮ͧ��ľ���EF��AE��FB=80+100=180�������ʱ����֮ͧ��ľ���Ϊ180���