��Ŀ����
����Ŀ�������������ߵĶ�����ͬ���������Ϊ���Ѻ������ߡ���������C1��y1=��2x2+4x+2��C2��u2=��x2+mx+nΪ���Ѻ������ߡ���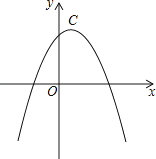
��1����������C2�Ľ���ʽ��
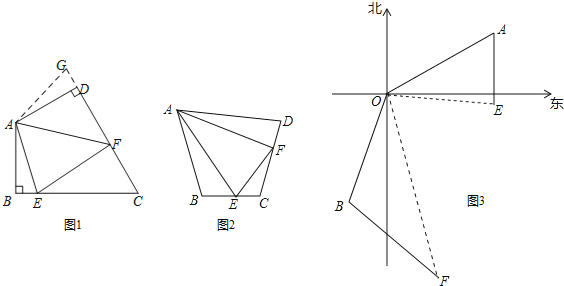
��2����A��������C2���ڵ�һ���Ķ��㣬��A��AQ��x�ᣬQΪ���㣬��AQ+OQ�����ֵ��
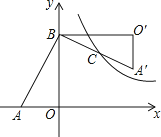
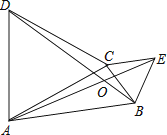
��3����������C2�Ķ���ΪC����B������Ϊ����1��4��������C2�ĶԳ������Ƿ���ڵ�M��ʹ�߶�MB�Ƶ�M��ʱ����ת90��õ��߶�MB�䣬�ҵ�B��ǡ������������C2�ϣ������������M�����꣬������˵�����ɣ�
���𰸡�
��1��
�⣺��y1=��2x2+4x+2=����2��x��1��2+4��
��������C1�Ķ�������Ϊ��1��4����
��������C1����C2������ͬ��
�� ![]() =1����1+m+n=4��
=1����1+m+n=4��
��ã�m=2��n=3��
��������C2�Ľ���ʽΪu2=��x2+2x+3
��2��
�⣺��ͼ1��ʾ��
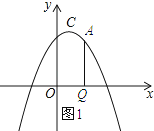
���A��������a����a2+2a+3����
��AQ=��a2+2a+3��OQ=a��
��AQ+OQ=��a2+2a+3+a=��a2+3a+3=����a�� ![]() ��2+
��2+ ![]() ��
��
�൱a= ![]() ʱ��AQ+OQ�����ֵ�����ֵΪ
ʱ��AQ+OQ�����ֵ�����ֵΪ ![]()
��3��
�⣺��ͼ2��ʾ������BC������B����B��D��CM������ΪD��

��B����1��4����C��1��4���������ߵĶԳ���Ϊx=1��
��BC��CM��BC=2��
�ߡ�BMB��=90�㣬
���BMC+��B��MD=90�㣮
��B��D��MC��
���MB��D+��B��MD=90�㣮
���MB��D=��BMC��
�ڡ�BCM�͡�MDB���У�  ��
��
���BCM�ա�MDB�䣮
��BC=MD��CM=B��D��
���M��������1��a������B��D=CM=4��a��MD=CB=2��
���B���������a��3��a��2����
�ੁ��a��3��2+2��a��3��+3=a��2��
�����ã�a2��7a��10=0��
���a=2����a=5��
��a=2ʱ��M������Ϊ��1��2����
��a=5ʱ��M������Ϊ��1��5����
������������M������Ϊ��1��2����1��5��ʱ��B��ǡ������������C2��
����������1�������y1�������꣬Ȼ���������������ߵĶ���������ͬ�����m��n��ֵ��
��2����A��a����a2+2a+3������OQ=x��AQ=��a2+2a+3��Ȼ��õ�OQ+AQ��a�ĺ�����ϵʽ����������䷽�������OQ+AQ����ֵ��
��3������BC������B����B��D��CM������ΪD��������֤����BCM�ա�MDB�䣬��ȫ�Ƚ��ε����ʵõ�BC=MD��CM=B��D�����M������Ϊ��1��a�������ú�a��ʽ�ӿɱ�ʾ����B������꣬����B���������������ߵĽ���ʽ�����a��ֵ���Ӷ��õ���M�����꣮

 �п������п��Ծ����ϵ�д�
�п������п��Ծ����ϵ�д� ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д�����Ŀ����һ���������У�С���ռ���ij���������˶����Ŷ���20����Աһ�����ߵIJ�������¼���£�
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
����20�����ݰ����1000���з��飬��ͳ�������������������в�������ͳ��ͼ����
��������ͳ�Ʊ�
��� | �������� | Ƶ�� |
A | 5500��x��6500 | 2 |
B | 6500��x��7500 | 10 |
C | 7500��x��8500 | m |
D | 8500��x��9500 | 3 |
E | 9500��x��10500 | n |
�����������Ϣ����������⣺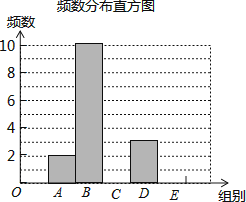
��1����գ�m= �� n=
��2����ȫƵ������ֱ��ͼ��
��3����20�����������˶����Ŷӳ�Աһ�����߲�������λ�������飻
��4�������Ŷӹ���120�ˣ����������һ�����߲���������7500����������