题目内容
【题目】如图，在菱形ABCD中，G是BD上一点，连接CG并延长交BA的延长线于点F，交AD于点E．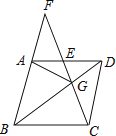
（1）求证：AG=CG．
（2）求证：AG2=GEGF．
【答案】
（1）
证明：∵四边形ABCD是菱形，
∴AB∥CD，AD=CD，∠ADB=∠CDB，
∴∠F∠FCD，
在△ADG与△CDG中， 
，
∴△ADG≌△CDG，
∴∠EAG=∠DCG，
∴AG=CG；
（2）
证明：∵△ADG≌△CDG，
∴∠EAG=∠F，
∵∠AGE=∠AGE，
∴△AEG∽△FGA，
∴ 
，
∴AG2=GEGF
【解析】根据菱形的性质得到AB∥CD，AD=CD，∠ADB=∠CDB，推出△ADG≌△CDG，根据全等三角形的性质即可得到结论；（2）由全等三角形的性质得到∠EAG=∠DCG，等量代换得到∠EAG=∠F，求得△AEG∽△FGA，即可得到结论．本题考查了相似三角形的判定和性质，菱形的性质，全等三角形的判定和性质，熟练掌握各定理是解题的关键．
【考点精析】解答此题的关键在于理解菱形的性质的相关知识，掌握菱形的四条边都相等；菱形的对角线互相垂直，并且每一条对角线平分一组对角；菱形被两条对角线分成四个全等的直角三角形；菱形的面积等于两条对角线长的积的一半，以及对相似三角形的判定与性质的理解，了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方．
练习册系列答案
相关题目
