Question

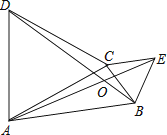
【题目】如图，矩形ABCD中，AB=9，AD=4．E为CD边上一点，CE=6．点P从点B出发，以每秒1个单位的速度沿着边BA向终点A运动，连接PE．设点P运动的时间为t秒．

（1）求△ADE的周长；

（2）当t为何值时，△PAE为直角三角形？

（3）是否存在这样的t，使EA恰好平分∠PED，若存在，求出t的值；若不存在，请说明理由．

Answer 1

【答案】（1）12；（2）t=6或t=；（3）t=；

【解析】

（1）在直角△ADE中，利用勾股定理进行解答；

（2）先利用勾股定理表示出PE2，在Rt△PAE中，根据勾股定理建立方程求解即可得出结论；

（3）利用角平分线的性质，平行线的性质以及等量代换推知：∠PEA=∠EAP，则PE=PA，由此列出关于t的方程，通过解方程求得相应的t的值即可．

解:（1）∵矩形ABCD中，AB=9，AD=4，

∴CD=AB=9，∠D=90°，

∴DE=9﹣6=3，

∴AE===5；

∴△ADE的周长为3+4+5=12

（2）①若∠EPA=90°，t=6；

②若∠PEA=90°，（6﹣t）2+42+52=（9﹣t）2，

解得t=．

综上所述，当t=6或t=时，△PAE为直角三角形；

（3）假设存在．

∵EA平分∠PED，∴∠PEA=∠DEA．

∵CD∥AB， ∴∠DEA=∠EAP，

∴∠PEA=∠EAP，

∴PE=PA，

∴（6﹣t）2+42=（9﹣t）2，

解得t=．

∴满足条件的t存在，此时t=．